设 ,先分别求
,先分别求 ,
, ,
, ,然后归纳猜想一般性结论,并给出证明.
,然后归纳猜想一般性结论,并给出证明.
设曲线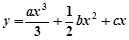 在点A(x,
在点A(x,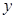 )处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x
)处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x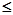 k (x)
k (x)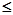
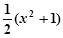 恒成立(
恒成立(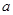 ≠0).
≠0).
(1) 求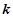 (1)的值;
(1)的值;
(2) 求函数k(x)的表达式;
(3) 求证: >
>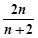
二项式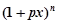 (
( 为大于零的常数)的展开式中各项的二项式系数之和为1024,按
为大于零的常数)的展开式中各项的二项式系数之和为1024,按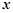 的升幂排列的前三项的系数之和是201.
的升幂排列的前三项的系数之和是201.
(1)求常数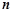 和
和 ;
;
(2)求该二项展开式中含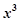 项的系数.
项的系数.
已知复数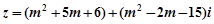 ,当实数
,当实数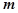 为何值时,
为何值时,
(1) 为实数; (2)
为实数; (2) 为虚数; (3)
为虚数; (3) 为纯虚数.
为纯虚数.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
(1)求直线 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(2)求 点到平面
点到平面 的距离
的距离
(3)线段 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
设命题 :方程
:方程 表示焦点在坐标轴上的双曲线,命题
表示焦点在坐标轴上的双曲线,命题 :
: 。
。
(1)写出命题 的否定;
的否定;
(2)若“ 或
或 ”为真命题,求实数
”为真命题,求实数 的取值范围。
的取值范围。
已知函数 (
( ,
, 为常数),且
为常数),且 为
为 的一个极值点.
的一个极值点.
(Ⅰ) 求 的值;
的值;
(Ⅱ) 求函数 的单调区间;
的单调区间;
(Ⅲ) 若函数 有3个不同的零点,求实数
有3个不同的零点,求实数 的取值范围.
的取值范围.
美国金融危机引发全球金融动荡,波及中国沪深两大股市,甲、乙、丙3人打算趁股市低迷之际买入股票。三人商定在圈定的10只股票中各自随机购买1只(假定购买时,每只股票的基本情况完全相同)
(1)求甲、乙、丙3人恰好买到相同股票的概率;
(2)求甲、乙、丙3人中至少有2人买到相同股票的概率.
已知圆 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 为参数)若直线
为参数)若直线 与圆
与圆 相切,求实数m的值.
相切,求实数m的值.