[浙江]2011-2012学年浙江省浙东北三校高二下学期期中联考理科数学试卷
6个人排成一排,其中甲、乙、丙三人必须站在一起的排列种数为( )
A. |
B. |
C. |
D. |
设函数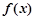 =(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则
=(x-a)(x-b)(x-c),(a,b,c是两两不等的常数),则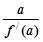 +
+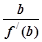 +
+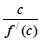 等于( )
等于( )
| A.0 | B.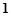 |
C.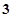 |
D.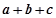 |
甲、乙、丙三人是同一家公司的职员,他们的妻子A、B、C也都是这家公司的职员。知情者介绍说:“A的丈夫是乙的好友,并在三个男子中最年轻;丙的年龄比C的丈夫大。”依据该知情者提供的信息,我们可以推出三对夫妻分别是( )
(A)甲—A,乙—B,丙—C (B)甲—A,乙—C,丙—B
(C)甲—B,乙—C,丙—A (D)甲—C,乙—B,丙—A
设[x]表示不超过x的最大整数(如[2]="2," [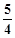 ]=1),对于给定的n
]=1),对于给定的n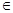 N*,定义
N*,定义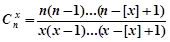 ,
,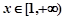 ,则当
,则当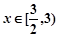 时,函数
时,函数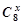 的值域是( )
的值域是( )
A.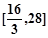 |
B.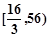 |
C.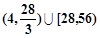 |
D.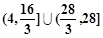 |
对于任意正整数n,定义“n的双阶乘n!!”如下:
当n是偶数时,n!!=n·(n-2)·(n-4)……6·4·2;
当n是奇数时,n!!=n·(n-2)·(n-4)……5·3·1
现在有如下四个命题:①(2003!!)·(2002!!)=2003!;②2002!!=21001·1001!;
③2002!!的个位数是0; ④2003!!的个位数是5.
其中正确的命题有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
将1,2,3填入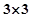 的方格中,要求每行、每列都没有重复数字(右面是一种填法),则不同的填写方法共有( )
的方格中,要求每行、每列都没有重复数字(右面是一种填法),则不同的填写方法共有( )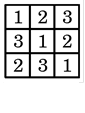
| A.48种 | B.24种 | C.12种 | D.6种 |
正五边形ABCDE,一个质点从正五边形的一个顶点出发沿着一条边移动到另一个顶点叫“移动一次”,则这个质点从A点开始,移动10次,又回到A点的移动方法共有 种。
二项式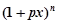 (
( 为大于零的常数)的展开式中各项的二项式系数之和为1024,按
为大于零的常数)的展开式中各项的二项式系数之和为1024,按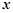 的升幂排列的前三项的系数之和是201.
的升幂排列的前三项的系数之和是201.
(1)求常数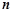 和
和 ;
;
(2)求该二项展开式中含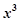 项的系数.
项的系数.
现有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,将这五个球放入5个盒子内.
(1)若只有一个盒子空着,共有多少种投放方法?
(2)若没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)若每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
已知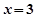 是函数
是函数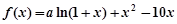 的一个极值点。
的一个极值点。
(1)求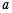 的值;
的值;
(2)求函数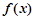 的单调区间;
的单调区间;
(3)若直线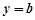 与函数
与函数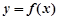 的图象有3个交点,求
的图象有3个交点,求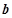 的取值范围。
的取值范围。
 = ( )
= ( )



 在(1,1)处的切线方程是( )
在(1,1)处的切线方程是( )




 展开后共有不同的项数为( )
展开后共有不同的项数为( ) 在区间
在区间 上的最小值为( )
上的最小值为( ) 与其共轭复数
与其共轭复数 满足:
满足: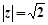 ,
,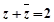 , 则( )
, 则( )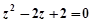
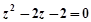
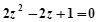
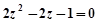
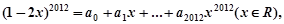 ,则
,则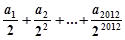 的值为( )
的值为( ) 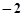
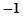
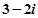 的虚部是 .
的虚部是 .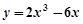 的极大值等于 .
的极大值等于 .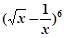 展开式中的常数项是 .
展开式中的常数项是 .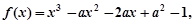 若要使方程
若要使方程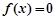 有且只有一个实根,则实数
有且只有一个实根,则实数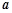 的取值范围是 .
的取值范围是 .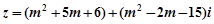 ,当实数
,当实数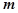 为何值时,
为何值时,
 为实数; (2)
为实数; (2)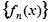 满足:
满足: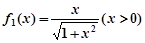 ,
,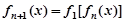
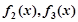 ;
;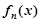 的表达式,并用数学归纳法证明你的结论
的表达式,并用数学归纳法证明你的结论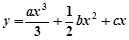 在点A(x,
在点A(x,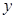 )处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x
)处的切线斜率为k(x),且k (-1)=0.对一切实数x,不等式x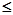 k (x)
k (x)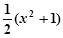 恒成立(
恒成立(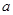 ≠0).
≠0).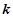 (1)的值;
(1)的值; >
>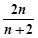
 粤公网安备 44130202000953号
粤公网安备 44130202000953号