(满分14分)设函数 .
.
(1)求 的单调区间;
的单调区间;
(2)若当 时,(其中
时,(其中 不等式
不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)试讨论关于x的方程: 在区间[0,2]上的根的个数.
在区间[0,2]上的根的个数.
(满分14分)如图,在四面体ABCD中,O、E分别是BD、BC的中点,

(Ⅰ)求证: 平面BCD;
平面BCD;
(Ⅱ)求异面直线AB与CD所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离.
(本小题满分14分)
已知等差数列{an}中,a1=-1,前12项和S12=186.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足 ,记数列{bn}的前n项和为Tn,
,记数列{bn}的前n项和为Tn,
求证: (n∈N*).
(n∈N*).
做投掷2颗骰子的试验,用(x,y)表示结果,其中x表示第1颗骰子出现的点数,y 表示第2颗骰子出现的点数,写出:
(1)求事件“出现点数相等”的概率 (2)求事件“出现点数之和大于8”的概率。
某射手在一次射击训练中,射中10环,9环,8环、7环的概率分别是0.21,0.23,0.25,0.28,计算这个射手在一次射击中:
(1)射中10环或7环的概率; (2)不够7环的概率。
已知数列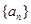 的前
的前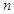 项和
项和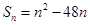
(1)求数列的通项公式 ;
(2)求 的最大或最小值
的最大或最小值
在等比数列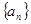 中,
中,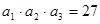 ,
,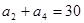
试求:(I)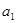 和公比
和公比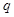 ;(II)前6项的和
;(II)前6项的和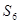 .
.
已知直线
(1) 当 时,求
时,求 与
与 的交点坐标;
的交点坐标;
(2) 过坐标原点O作 的垂线,垂足为A,P为OA的中点,当
的垂线,垂足为A,P为OA的中点,当 变化时,求P点的轨迹的参数方程,
变化时,求P点的轨迹的参数方程,
(3) 并指出它是什么曲线。
在平面直角坐标系中,求方程 所对应的直线经过伸缩变换
所对应的直线经过伸缩变换 后的直线方程。
后的直线方程。
已知函数
(1)指出 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(2)用五点法画出它在一个周期内的闭区间上的图象;
(3)说明此函数图象可由 的图象经怎样的变换得到.
的图象经怎样的变换得到.