高中数学解答题

（满分10分）
已知，求下列各式的值：(1) （2）

（满分12分）
已知函数的最大值为，最小值为，求函数的最值.

（本小题满分14分）
已知函数，如果存在给定的实数对（），使得恒成立，则称为“S-函数”.
（Ⅰ）判断函数是否是“S-函数”；
（Ⅱ）若是一个“S-函数”，求出所有满足条件的有序实数对；
（Ⅲ）若定义域为的函数是“S-函数”，且存在满足条件的有序实数对和，当时，的值域为，求当时函数的值域.

（本小题满分13分）
已知的顶点A、B在椭圆
（Ⅰ）当AB边通过坐标原点O时，求AB的长及的面积；
（Ⅱ）当，且斜边AC的长最大时，求AB所在直线的方程.

（本小题满分14分）
已知函数，
（Ⅰ）若时，求曲线在点处的切线方程；
（Ⅱ）若函数在上是减函数，求实数的取值范围；
（Ⅲ）令，是否存在实数，当（是自然对数的底）时，函数 的最小值是3，若存在，求出的值；若不存在，说明理由．

（本小题满分13分）
设数列的前项和为，已知， （
（Ⅰ）求的表达式；
（Ⅱ）若数列的前项和为，问：满足的最小正整数是多少？

（本小题满分13分）
已知角的顶点在原点，始边与轴的正半轴重合，终边经过点.
（Ⅰ）求的值；
（Ⅱ）若函数，
求函数在区间上的取值范围．

如图，已知向量，可构成空间向量的一个基底，若，在向量已有的运算法则的基础上，新定义一种运算，显然的结果仍为一向量，记作．
1、求证：向量为平面的法向量；
2、求证：以为边的平行四边形的面积等于；
将四边形按向量平移，得到一个平行六面体，试判断平行六面体的体积与的大小．

如图，圆柱OO内有一个三棱柱ＡＢＣ—Ａ，三棱柱的底面为圆柱底面的内接三角形，且AB是圆O直径。
(1)证明：平面平面;
(2)设ＡＢ=ＡＡ,在圆柱ＯＯ内随机选取一点，记该点取自三棱柱ＡＢＣ—ＡＢ内的概率为Ｐ.
①当点C在圆周上运动时，求的最大值；
②记平面与平面所成的角为，当取最大值时，求的值。

设函数.
（1）  试问函数能否在时取得极值？说明理由；
（2）  若a=-1，当时，函数与的图像有两个公共点，求c的取值范围

某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场，其总面积为3000平方米，其中场地四周（阴影部分）为通道，通道宽度均为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为S平方米.
（1）  分别写出用x表示y和S的函数关系式（写出函数定义域）怎样设计能使s取得最大值，最大值为多少？

在数列中，，若函数在点处切线过点（）
（1）  求证：数列为等比数列；
求数列的通项公式和前n项和公式.

（本小题满分14分）
某商店经营的消费品进价每件14元，月销售量Q（百件）与销售价格P（元）的关系如下图，每月各种开支2000元，
（1）写出月销售量Q（百件）与销售价格P（元）的函数关系。
（2）该店为了保证职工最低生活费开支3600元，问：商品价格应控制在什么范围？
（3）当商品价格每件为多少元时，月利润并扣除职工最低生活费的余额最大？并求出最大值。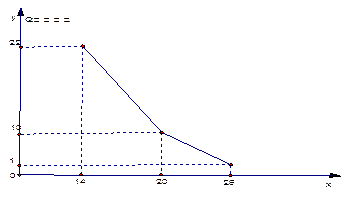

．（本小题满分12分）直线l经过点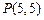，且和圆C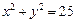：相交，截得弦长为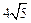，求l的方程．

（本小题满分12分）
已知函数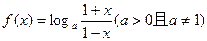
（1）求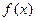的定义域；
（2）判断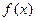的奇偶性并证明；