如图，已知向量
，可构成空间向量的一个基底，若
，在向量已有的运算法则的基础上，新定义一种运算
，显然
的结果仍为一向量，记作
．
1、求证：向量为平面
的法向量；
2、求证：以
为边的平行四边形
的面积等于
；
将四边形按向量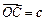
平移，得到一个平行六面体
，试判断平行六面体的体积
与
的大小．
抛物线的标准方程。
上一点
，它到左准线的距离为
，求点
上任何一点到两条渐近线的距离之积为定值．
的一底边
在平面
内，另一底边
在平面
到平面
，若
，求
到平面
的左、右两个焦点分别为
，点
在双曲线上，且
，求
的面积．推荐套卷
如图，已知向量，可构成空间向量的一个基底，若，在向量已有的运算法则的基础上，新定义一种运算，显然的结果仍为一向量，记作．
1、求证：向量为平面的法向量；
2、求证：以为边的平行四边形的面积等于；
将四边形按向量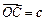平移，得到一个平行六面体，试判断平行六面体的体积与的大小．
粤公网安备 44130202000953号