(本小题满分12分)
若非零函数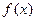 对任意实数
对任意实数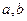 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当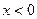 时,
时,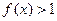 .
.
(1)求证: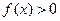
(2)求证: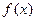 为减函数;
为减函数;
(3)当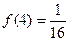 时,解不等式
时,解不等式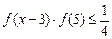
(本小题满分12分)
求经过两条直线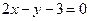 和
和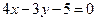 的交点,并且与直线
的交点,并且与直线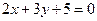 垂直的直线方程(一般式).
垂直的直线方程(一般式).
已知向量:a=(2sinx,2 sinx),b=(sinx, cosx).
cosx).
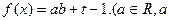 为常数)
为常数)
(1)若 ,求
,求 的最小正周期;
的最小正周期;
(2)若 在[
在[ 上最大值与最小值之和为5,求t的值;
上最大值与最小值之和为5,求t的值;
(3)在(2)条件下 先按
先按 平移后(︱
平移后(︱ ︱最小)再经过伸缩变换后得到
︱最小)再经过伸缩变换后得到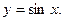 求
求 .
.
已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.
(1)求实数m的取值范围;(2)求该圆半径r的取值范围;(3)求圆心的轨迹方程.
(本小题满分15分)已知直线l的方程为: ,直线l与x轴的交点为F, 圆O的方程为:
,直线l与x轴的交点为F, 圆O的方程为: ,C、 D在圆上, CF⊥DF,设线段CD的中点为M.
,C、 D在圆上, CF⊥DF,设线段CD的中点为M.
(1)如果CFDG为平行四边形,求动点G的轨迹;
(2)已知椭圆的中心在原点,右焦点为F,直线l交椭圆于A、B两点,又 ,
,
求椭圆C的方程.
(本小题满分15分)
函数 ,曲线
,曲线 上点
上点 处的切线方程为
处的切线方程为
(1)若 在
在 时有极值,求函数
时有极值,求函数 在
在 上的最大值;
上的最大值;
(2)若函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
(本小题满分14分)
数列{ }满足递推式
}满足递推式 ,其中
,其中 .
.
(1)求a1,a2;
(2)是否存在一个实数 ,使得
,使得 为等差数列,如果存在,求出
为等差数列,如果存在,求出 的值;如果不存在,试
的值;如果不存在,试
说明理由;
(3)求数列{ }的前n项之和.
}的前n项之和.
(本小题满分14分)
已知向量 ,向量
,向量 与
与 的夹角为
的夹角为 , 且
, 且 .
.
(1)求向量 ;
;
(2)若 且
且

 ,
, ,其中A、C是
,其中A、C是 的内角,若三角形的三个内角A、B、C依次成等差数列,试求
的内角,若三角形的三个内角A、B、C依次成等差数列,试求 的取值范围
的取值范围
(本小题满分14分)
在锐角△ABC中,已知 .
.
(1)求 的最大值;
的最大值;
(2)当 取得最大值时,
取得最大值时, ,如果
,如果 ,求
,求 边和
边和 边的长.
边的长.
(本题14分)数列 的前
的前 项和为
项和为 ,已知
,已知
(1)证明:数列 是等差数列,并求
是等差数列,并求 ;
;
(2)设 ,求证:
,求证: .
.
(本题14分)(如右图)半径为1,圆心角为 的扇形,点
的扇形,点 是扇形AB弧上的动点,设
是扇形AB弧上的动点,设 .
.
(1)用x表示平行四边形ODPC的面积 ;
;
(2)求平行四边形ODPC面积的最大值.
(本题14分)设集合 ,
,
(1)当 时,求A的非空真子集的个数
时,求A的非空真子集的个数
(2)若 ,求实数m的取值范围.
,求实数m的取值范围.