(1)已知抛物线的顶点在原点,准线方程为 ,求抛物线的标准方程;
,求抛物线的标准方程;
(2)已知双曲线的焦点在x轴上,且过点( ,-
,- ),(
),( ,
, ),求双曲线的标准方程。
),求双曲线的标准方程。
(本小题满分12分)为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝 以上为“常喝”,体重超过
以上为“常喝”,体重超过 为“肥胖”.
为“肥胖”.
| |
常喝 |
不常喝 |
合计 |
| 肥胖 |
|
2 |
|
| 不肥胖 |
|
18 |
|
| 合计 |
|
|
30 |
已知在全部 人中随机抽取1人,抽到肥胖的学生的概率为
人中随机抽取1人,抽到肥胖的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
参考数据:
 |
0.150 |
0.100 |
0.050 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分13分)已知函数
(1)若对任意 ,
, 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
(2)当 时,求函数
时,求函数 的最小值
的最小值
(本小题满分15分)已知 ,
, ,
, 分别是
分别是 的内角
的内角 所对的边,且
所对的边,且 ,
, .
.
(1)求角 的大小;
的大小;
(2)若 ,求边
,求边 的长.
的长.
(本小题满分12分)定义 的零点
的零点 为
为 的不动点,已知函数
的不动点,已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 的不动点;
的不动点;
(Ⅱ)对于任意实数 ,函数
,函数 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数 的取值范围;
的取值范围;
(Ⅲ)若函数 只有一个零点且
只有一个零点且 ,求实数
,求实数 的最小值.
的最小值.
(本题满分14分,第1小题6分,第2小题8分)
已知函数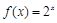 的反函数为
的反函数为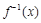
(1)若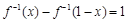 ,求实数
,求实数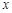 的值;
的值;
(2)若关于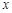 的方程
的方程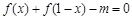 在区间
在区间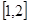 内有解,求实数
内有解,求实数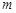 的取值范围;
的取值范围;
(本小题满分16分)已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式>2 010的n的最小值.
(本题小满分12分)
如图,平面四边形 中,角
中,角 ,且
,且 .
.
(Ⅰ)求∠ ;
;
(Ⅱ)求四边形 的面积
的面积 .
.