已知函数 在
在 处取得极值.
处取得极值.
(1)求 的值;
的值;
(2)求函数 在
在 上的最小值;
上的最小值;
(3)求证:对任意 、
、 ,都有
,都有 .
.
(本小题满分15分)已知 是复数,若
是复数,若 为实数(
为实数( 为虚数单位),且
为虚数单位),且 为纯虚数.
为纯虚数.
(1)求复数 ;
;
(2)若复数 在复平面上对应的点在第四象限,求实数
在复平面上对应的点在第四象限,求实数 的取值范围
的取值范围
【原创】(本小题满分14分)设集合 ,
, ,
, .
.
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若 且
且 ,求实数
,求实数 的取值范围.
的取值范围.
【原创】设函数
(1)若 为函数
为函数 的极值点,求
的极值点,求 的值
的值
(2)在(1)的条件下,函数 的图象的对称中心为
的图象的对称中心为 ,求
,求 的值;
的值;
如图,AB为圆O的切线,A为切点,C为线段AB的中点,过C作圆O的割线CED(E在C,D之间),求证:∠CBE=∠BDE.
(本小题满分14分)设函数 ,
,
(1)证明: 是
是 上的增函数;
上的增函数;
(2)设 ,当
,当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
己知斜三棱柱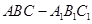 的底面是边长为
的底面是边长为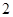 的正三角形,侧面
的正三角形,侧面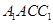 为菱形,
为菱形,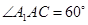 ,平面
,平面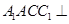 平面
平面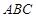 ,
,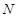 是
是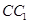 的中点.
的中点.
(1)求证: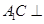
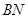 ;
;
(2)求二面角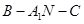 的余弦值.
的余弦值.