甘肃省部分普通高中高三第一次联考理科数学试卷
下面是关于复数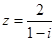 的四个命题:
的四个命题: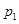 :
: ,
, 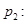
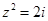
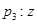 的共轭复数为
的共轭复数为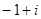
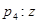 的虚部为
的虚部为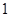
其中真命题为( )
A.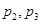 |
B.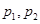 |
C.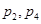 |
D.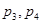 |
下列推断错误的是( )
A.命题“若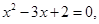 则 则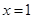 ”的逆否命题为“若 ”的逆否命题为“若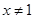 则 则 ” ” |
B.命题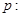 存在 存在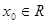 ,使得 ,使得 ,则非 ,则非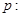 任意 任意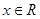 ,都有 ,都有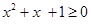 |
C.若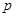 且 且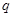 为假命题,则 为假命题,则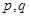 均为假命题 均为假命题 |
D.“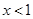 ”是“ ”是“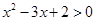 ”的充分不必要条件 ”的充分不必要条件 |
若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示,则这个棱柱的体积为( )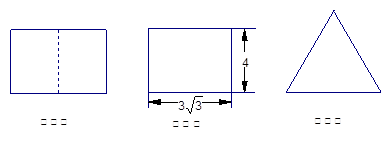
A. |
B.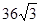 |
C.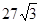 |
D.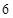 |
抛物线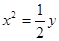 在第一象限内图象上一点
在第一象限内图象上一点 处的切线与
处的切线与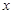 轴交点的横坐标记
轴交点的横坐标记
为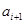 ,其中
,其中 ,若
,若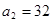 ,则
,则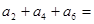 ( )
( )
A.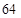 |
B.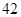 |
C.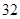 |
D.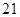 |
定义行列式运算: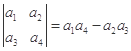 .若将函数
.若将函数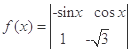 的图象向左平移
的图象向左平移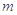
 个单位后,所得图象对应的函数为奇函数,则
个单位后,所得图象对应的函数为奇函数,则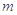 的最小值是( )
的最小值是( )
A.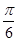 |
B.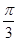 |
C.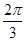 |
D.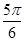 |
设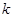 是一个正整数,
是一个正整数,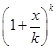 的展开式中第四项的系数为
的展开式中第四项的系数为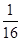 ,记函数
,记函数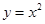 与
与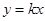 的图像所围成的阴影部分为
的图像所围成的阴影部分为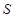 ,任取
,任取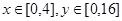 ,则点
,则点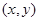 恰好落在阴影区域内的概率为( )
恰好落在阴影区域内的概率为( )
A.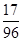 |
B.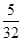 |
C.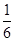 |
D.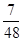 |
已知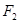 、
、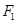 是双曲线
是双曲线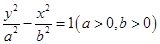 的上、下焦点,点
的上、下焦点,点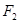 关于渐近线的对称点恰好落在以
关于渐近线的对称点恰好落在以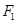 为圆心,
为圆心,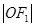 为半径的圆上,则双曲线的离心率为( )
为半径的圆上,则双曲线的离心率为( )
A.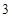 |
B.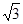 |
C.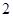 |
D.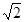 |
正四棱锥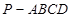 的五个顶点在同一球面上,若正四棱锥的底面边长是
的五个顶点在同一球面上,若正四棱锥的底面边长是 ,侧棱长为
,侧棱长为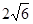 ,则此球的表面积___________.
,则此球的表面积___________.
从某校数学竞赛小组的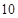 名成员中选
名成员中选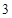 人参加省级数学竞赛,则甲、乙
人参加省级数学竞赛,则甲、乙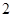 人至少有
人至少有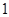 人入选,而丙没有入选的不同选法的种数为 (用数字作答).
人入选,而丙没有入选的不同选法的种数为 (用数字作答).
在平面直角坐标系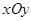 中,圆
中,圆 的方程为
的方程为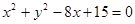 ,若直线
,若直线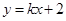 上至少存在一点,使得以该点为圆心,半径为
上至少存在一点,使得以该点为圆心,半径为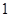 的圆与圆
的圆与圆 有公共点,则
有公共点,则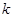 的最小值是____.
的最小值是____.
(本小题满分12分)甲乙两人进行围棋比赛,约定每局胜者得1分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多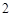 分或打满
分或打满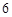 局时停止.设甲在每局中获胜的概率
局时停止.设甲在每局中获胜的概率
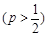 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为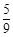 .
.
(1)求 的值;
的值;
(2)设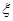 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量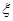 的分布列和数学期望
的分布列和数学期望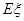 .
.
己知斜三棱柱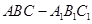 的底面是边长为
的底面是边长为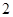 的正三角形,侧面
的正三角形,侧面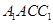 为菱形,
为菱形,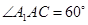 ,平面
,平面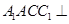 平面
平面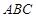 ,
,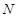 是
是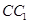 的中点.
的中点.
(1)求证: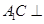
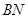 ;
;
(2)求二面角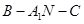 的余弦值.
的余弦值.
已知椭圆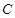 的对称中心为原点
的对称中心为原点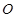 ,焦点在
,焦点在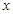 轴上,左右焦点分别为
轴上,左右焦点分别为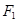 和
和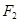 ,且
,且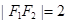 ,点
,点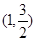 在该椭圆上.
在该椭圆上.
(1)求椭圆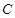 的方程;
的方程;
(2)过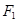 的直线
的直线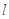 与椭圆
与椭圆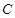 相交于
相交于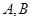 两点,若
两点,若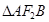 的面积为
的面积为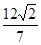 ,求以
,求以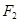 为圆心且与直线
为圆心且与直线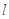 相切圆的方程.
相切圆的方程.
(本小题满分12分)已知函数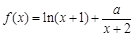
(1)当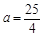 时,求
时,求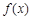 的单调递减区间;
的单调递减区间;
(2)若当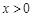 时,
时,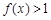 恒成立,求
恒成立,求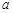 的取值范围;
的取值范围;
(3)求证:

(本小题满分10分)选修4—1:几何证明选讲
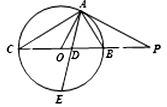
如图所示,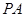 为圆
为圆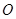 的切线,
的切线,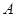 为切点,
为切点,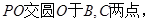
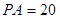 ,
,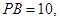
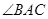 的角平分线与
的角平分线与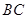 和圆
和圆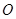 分别交于点
分别交于点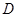 和
和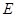 .
.
(1)求证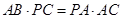
(2)求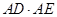 的值.
的值.
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系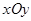 中,圆
中,圆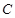 的参数方程
的参数方程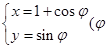 为参数).以
为参数).以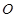 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆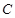 的极坐标方程;
的极坐标方程;
(2)直线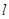 的极坐标方程是
的极坐标方程是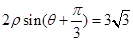 ,射线
,射线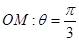 与圆
与圆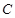 的交点为
的交点为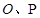 ,与直线
,与直线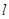 的交点为
的交点为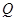 ,求线段
,求线段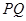 的长.
的长.
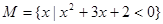 ,集合
,集合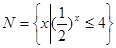 , 则
, 则 ( )
( )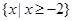
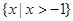
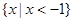

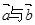 的夹角为
的夹角为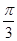 ,
,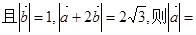 ( )
( )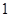
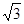
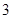
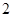
 中,
中,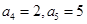 ,则数列
,则数列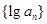 的前8项和等于( )
的前8项和等于( )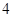

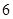
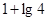
 满足不等式组
满足不等式组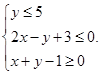 则
则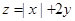 的最大值是( )
的最大值是( )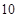
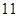
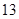
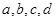 满足
满足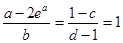 其中
其中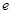 是自然对数的底数,则
是自然对数的底数,则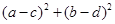 的最小值为( )
的最小值为( )

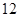
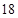
 ,
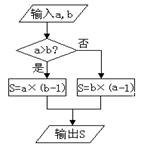
, 的运算原理如右图:则式子
的运算原理如右图:则式子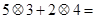 _________.
_________.
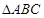 中,角
中,角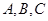 的对边分别为
的对边分别为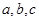 且
且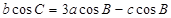
 的值;
的值;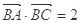 ,且
,且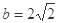 ,求
,求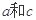 的值.
的值.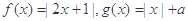
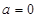 时,解不等式
时,解不等式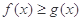 ;
;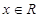 ,使得,
,使得, 成立,求实数
成立,求实数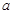 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号