高中数学解答题

（本小题满分12分）已知函数.
（1）若函数满足,且在定义域内恒成立，求实数b的取值范围；
（2）若函数在定义域上是单调函数，求实数a的取值范围；
（3）当时，试比较与的大小.

化简或求值:
（1） ；
（2）

设集合至多有个一元素，求实数的取值范围.

（本小题满分12分）下图是调查某地某公司1000名员工的月收入后制作的直方图.根据直方图估计：

（Ⅰ）该公司月收入在1000元到1500元之间的人数;
（Ⅱ）该公司员工的月平均收入;
（Ⅲ）该公司员工收入的众数;
（Ⅳ）该公司员工月收入的中位数;

甲、乙两位学生参加数学竞赛培训，在培训期间他们参加的次预赛成绩记录如下：甲：，，， ，  乙：，，，，
（1）用茎叶图表示这两组数据；（2）求甲、乙两人的成绩的平均数与方差;
（3）若现要从中选派一人参加数学竞赛，你认为选派哪位学生参加合适说明理由？

知二次函数，在区间上恰有一个零点，解不等式.

已知首项都是1的两个数列{a_n}，{b_n}（b_n≠0，n∈N^*）
满足a_nb_n＋1－a_n＋1b_n＋2b_n＋1b_n＝0．
（1）令c_n＝，求数列{c_n}的通项公式；
（2）若b_n＝3^n－1，求数列{a_n}的前n项和S_n．

已知椭圆的中心在坐标原点，焦点在轴上，离心率为，椭圆上的点到焦点距离的最大值为．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若过点的直线与椭圆交于不同的两点，且，求实数 的取值范围．

已知全集为,集合，集合.
求：（Ⅰ）；           （Ⅱ）．

如图，是正方形，是正方形的中心，底面，是的中点．求证：（1）//平面；（2）平面平面．

(本小题满分12分)为了宣传今年10月在某市举行的“第十届中国艺术节”， “十艺节”筹委会举办了“十艺节”知识有奖问答活动，随机对市民15～65岁的人群抽样n人，回答问题统计结果如下图表所示：

（Ⅰ）分别求出a，x的值；
（Ⅱ）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，“十艺节”筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率．

已知命题函数在上单调递增，命题：函数在R上是增函数.
（1）若或为真命题，求的取值范围；
（2）若或为真命题，求的取值范围.

等比数列的首项为，公比为，用表示这个数列的第n项到第m项共项的和．
（Ⅰ）计算，，，并证明它们仍成等比数列；
（Ⅱ）受上面（Ⅰ）的启发，你能发现更一般的规律吗？写出你发现的一般规律，并证明．

（本小题满分12分）如图,,动点与分别在射线上,且线段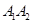的长为1,线段的长为2,点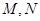分别是线段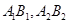的中点.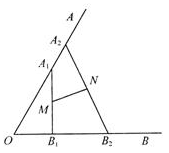

（Ⅰ）用向量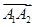与表示向量;
（Ⅱ）求向量的模.

如图，已知四棱锥，底面为菱形，平面，，分别是的中点．

（1）证明：；
（2）若,求二面角的余弦值．