浙江省温州市十校联合体高三上学期期中联考理科数学试卷
设 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的 的值是( )
的值是( )
| A.2 | B. |
C. |
D.3 |
设 是两条不同的直线,
是两条不同的直线,  是两个不同的平面,下列命题中错误的是( )
是两个不同的平面,下列命题中错误的是( )
A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , ,则 ,则 |
D.若 , , , , ,则 ,则 |
将函数 的图象向左平移
的图象向左平移 个单位,再向下平移1个单位,得到函
个单位,再向下平移1个单位,得到函
数 的图象,则
的图象,则 的解析式为( )
的解析式为( )
A. |
B. |
C. |
D. |
设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心,|FM|为半径的圆和抛物线的准线相交,则y0的取值范围是 ( )
| A.(0,2) | B.[0,2] | C.(2,+∞) | D.[2,+∞) |
设等差数列 的前
的前 项和为
项和为 ,若
,若 ,则满足
,则满足 的正整数
的正整数 的值为( )
的值为( )
| A.13 | B.12 | C.11 | D.10 |
若 是一个集合,
是一个集合, 是一个以
是一个以 的某些子集为元素的集合,且满足:①
的某些子集为元素的集合,且满足:① 属于
属于 ,
, 属于
属于 ;②
;② 中任意多个元素的并集属于
中任意多个元素的并集属于 ;③
;③ 中任意多个元素的交集属于
中任意多个元素的交集属于 .则称
.则称 是集合
是集合 上的一个拓扑.已知集合
上的一个拓扑.已知集合 ,对于下面给出的四个集合
,对于下面给出的四个集合 :
:
① ;
;
② ;
;
③ ;
;
④ .
.
其中是集合 上的拓扑的集合
上的拓扑的集合 的序号是( )
的序号是( )
| A.① | B.② | C.②③ | D.②④ |
过双曲线 的左焦点F作圆
的左焦点F作圆 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 为
为 的中点,则双曲线的离心率为________.
的中点,则双曲线的离心率为________.
函数 ,其中
,其中 ,若动直线
,若动直线 与函数
与函数 的图像有三个不同的交点,它们的横坐标分别为
的图像有三个不同的交点,它们的横坐标分别为 ,则
,则 是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”______________.
是否存在最大值?若存在,在横线处填写其最大值;若不存在,直接填写“不存在”______________.
已知函数 .
.
(1)求该函数图象的对称轴;
(2)在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,求
,求 的取值范围.
的取值范围.
已知等差数列 的各项均为正数,
的各项均为正数, ,其前
,其前 项和为
项和为 ,
, 为等比数列,
为等比数列,  ,且
,且 .
.
(1)求 与
与 ;
;
(2)若 对任意正整数
对任意正整数 和任意
和任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
如图,已知四棱锥 ,底面
,底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.

(1)证明: ;
;
(2)若 ,求二面角
,求二面角 的余弦值.
的余弦值.
已知椭圆 :
: 的离心率
的离心率 ,并且经过定点
,并且经过定点 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为椭圆
为椭圆 的左右顶点,
的左右顶点, 为直线
为直线 上的一动点(点
上的一动点(点 不在x轴上),连
不在x轴上),连 交椭圆于
交椭圆于 点,连
点,连 并延长交椭圆于
并延长交椭圆于 点,试问是否存在
点,试问是否存在 ,使得
,使得 成立,若存在,求出
成立,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 ,
, ,则
,则 ( )
( )



 是二次函数,
是二次函数, ,若函数
,若函数 的值域是
的值域是 ,则函数
,则函数


 ,若实数
,若实数 满足
满足 ,则( )
,则( )



 则
则 =_______________.
=_______________. )为平面区域
)为平面区域 上的一个动点,则
上的一个动点,则 的最大值是_______.
的最大值是_______. 的前
的前 项和
项和 ,则
,则 =___________.
=___________.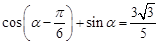 ,则
,则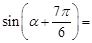 .
. 是单位向量,
是单位向量, .若向量
.若向量 满足
满足 ______.
______. .
. 为偶函数,求
为偶函数,求 的值;
的值; ,求函数
,求函数 时,若对任意的
时,若对任意的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号