等比数列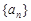 的首项为
的首项为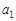 ,公比为
,公比为 ,用
,用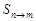 表示这个数列的第n项到第m项共
表示这个数列的第n项到第m项共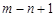 项的和.
项的和.
(Ⅰ)计算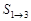 ,
,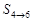 ,
, ,并证明它们仍成等比数列;
,并证明它们仍成等比数列;
(Ⅱ)受上面(Ⅰ)的启发,你能发现更一般的规律吗?写出你发现的一般规律,并证明.
相关知识点
推荐套卷
等比数列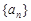 的首项为
的首项为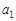 ,公比为
,公比为 ,用
,用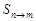 表示这个数列的第n项到第m项共
表示这个数列的第n项到第m项共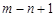 项的和.
项的和.
(Ⅰ)计算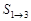 ,
,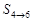 ,
, ,并证明它们仍成等比数列;
,并证明它们仍成等比数列;
(Ⅱ)受上面(Ⅰ)的启发,你能发现更一般的规律吗?写出你发现的一般规律,并证明.