高中数学组合几何解答题

（本小题14分） 已知函数，若
（1）求曲线在点处的切线方程；
（2）若函数在区间上有两个零点，求实数b的取值范围；
（3）当

已知,
（Ⅰ）当时，求曲线在点处的切线方程；
（Ⅱ）若在处有极值，求的单调递增区间；
（Ⅲ）是否存在实数，使在区间的最小值是3，若存在，求出的值；若不存在，说明理由.

已知函数（为常数），且在点处的切线平行于轴．
（Ⅰ）求实数的值；
（Ⅱ）求函数的单调区间．

已知函数，且在处的切线方程为.
（1）求的解析式；
（2）证明：当时，恒有；
（3）证明：若，，且，则.

如下图，过曲线：上一点作曲线的切线交轴于点，又过作 轴的垂线交曲线于点，然后再过作曲线的切线交轴于点，又过作轴的垂线交曲线于点，，以此类推，过点的切线 与轴相交于点，再过点作轴的垂线交曲线于点（N）．
(1) 求、及数列的通项公式；(2) 设曲线与切线及直线所围成的图形面积为，求的表达式； (3) 在满足(2)的条件下, 若数列的前项和为，求证：N.

已知函数，当时，取得极大值；当时，取得极小值．
求、、的值;
求在处的切线方程．

已知曲线与在处的切线互相垂直,求的值.

已知函数 , .  
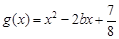（Ⅰ）当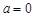时，求曲线在点处的切线方程；
（Ⅱ）当时，求函数的单调区间；
（Ⅲ）当时，函数在上的最大值为，若存在，使得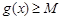成立，求实数b的取值范围.

已知，其中是自然常数，
（1）讨论时, 的单调性、极值；
（2）是否存在实数，使的最小值是3，若存在，求出的值；若不存在，说明理由.

已知函数f (x) =
（1）试判断当的大小关系；
（2）试判断曲线和是否存在公切线，若存在，求出公切线方程，若不存在，说明理由；
（3）试比较 (1 + 1×2) (1 + 2×3) ……（1 +2012×2013)与的大小，并写出判断过程．

已知是二次函数，不等式的解集是，且在点处的切线与直线平行.求的解析式；

函数，其中为常数，且函数和
的图象在其与坐标轴的交点处的切线互相平行，求此时平行线的距离。

曲线在点处的切线与x轴交点的横坐标为a_n．
（1）求a_n；
（2）设，求数到的前n项和S_n．

已知函数为大于零的常数。
（1）若函数内调递增，求a的取值范围；
（2）求函数在区间[1，2]上的最小值。

设函数在及时取得极值．
（1）求、b的值；
（2）若对于任意的，都有成立，求c的取值范围．