[四川]2012-2013学年四川成都六校协作体高二下学期期中考试理科数学试卷
命题“若α=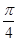 ,则tanα=1”的逆否命题是
,则tanα=1”的逆否命题是
A.若α≠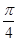 ,则tanα≠1 ,则tanα≠1 |
B.若α=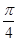 ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠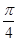 |
D.若tanα≠1,则α=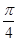 |
已知命题p: x1,x2
x1,x2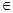 R,(f(x2)
R,(f(x2) f(x1))(x2
f(x1))(x2 x1)≥0,则
x1)≥0,则 p是
p是
A. x1,x2 x1,x2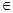 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)≤0 x1)≤0 |
B. x1,x2 x1,x2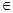 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)≤0 x1)≤0 |
C. x1,x2 x1,x2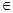 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)<0 x1)<0 |
D. x1,x2 x1,x2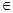 R,(f(x2) R,(f(x2) f(x1))(x2 f(x1))(x2 x1)<0 x1)<0 |
设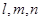 均为直线,其中
均为直线,其中 在平面
在平面 内,则
内,则 是
是 且
且 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知F1、F2为双曲线C:x²-y²=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=( )
A. |
B. |
C.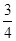 |
D. |
已知函数f(x)=x2+2x+blnx,若函数f(x)在(0,1)上单调,则实数b的取值范围是
| A.b≥ 0 | B.b<-4 | C.b≥0或b≤-4 | D.b>0或b<-4 |
抛物线 的焦点为
的焦点为 ,点
,点 为抛物线上的动点,点
为抛物线上的动点,点 为其准线上的动点,当
为其准线上的动点,当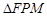 为等边三角形时,其面积为
为等边三角形时,其面积为
A. |
B.4 | C.6 | D. |
已知 是定义在
是定义在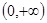 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则
,则 的大小关系为
的大小关系为
A. |
B. |
C. |
D.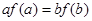 |
已知抛物线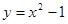 上一定点B(-1,0)和两个动点
上一定点B(-1,0)和两个动点 ,当
,当 时,点
时,点 的横坐标的取值范围是
的横坐标的取值范围是
A. ∪ ∪  |
B. |
C. |
D.(-∞,-3]∪ |
椭圆 =1上一点P与椭圆的两个焦点F1、F2的连线互相垂直,则△PF1F2的面积为_____________
=1上一点P与椭圆的两个焦点F1、F2的连线互相垂直,则△PF1F2的面积为_____________
函数f(x)= ex(sinx+cosx)在x∈
ex(sinx+cosx)在x∈ 上的值域为 _____________
上的值域为 _____________
在直角坐标系 中,点
中,点 与点
与点 关于原点
关于原点 对称.点
对称.点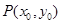 在抛物线
在抛物线 上,且直线
上,且直线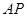 与
与 的斜率之积等于-
的斜率之积等于- ,则
,则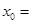 _____________
_____________
已知下列几个命题: ①已知F1、F2为两定点, =4,动点M满足
=4,动点M满足 ,则动点M的轨迹是椭圆。 ②一个焦点为
,则动点M的轨迹是椭圆。 ②一个焦点为 且与双曲线
且与双曲线 有相同的渐近线的双曲线标准方程是
有相同的渐近线的双曲线标准方程是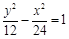 ③“若
③“若 =b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线
=b,则a2=ab”的否命题。④若一个动圆的圆心在抛物线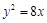 上,且动圆恒与直线
上,且动圆恒与直线 相切,则动圆必过定点
相切,则动圆必过定点 。
。
其中真命题有____________
过点 的直线
的直线 与抛物线
与抛物线 交于
交于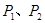 两点,记线段
两点,记线段 的中点为
的中点为 ,过点
,过点 和这个抛物线的焦点
和这个抛物线的焦点 的直线为
的直线为 ,
, 的斜率为
的斜率为 ,则直线
,则直线 的斜率与直线
的斜率与直线 的斜率之比可表示为
的斜率之比可表示为 的函数
的函数 __ .
__ .
已知焦距为 的双曲线的焦点在x轴上,且过点P
的双曲线的焦点在x轴上,且过点P .
.
(Ⅰ)求该双曲线方程 ;
(Ⅱ)若直线m经过该双曲线的右焦点且斜率为1,求直线m被双曲线截得的弦长.
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x (单位:元/千克)满足关系式y= +10(x-6)2,(其中3<x<6,
+10(x-6)2,(其中3<x<6, 为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数,)已知销售价格为5元/千克时,每日可售出该商品11千克。
(I)求 的值;
的值;
(II)若该商品的成品为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
如图,四边形 与
与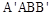 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是 的中点,
的中点,

求证: ;
;
求证:平面 ;
;
求体积 与
与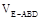 的比值。
的比值。
已知函数 ,
, 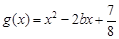 .
.
(Ⅰ)当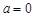 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当 时,函数
时,函数 在
在 上的最大值为
上的最大值为 ,若存在
,若存在 ,使得
,使得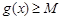 成立,求实数b的取值范围.
成立,求实数b的取值范围.
 在点
在点 处的切线经过点
处的切线经过点 ,则
,则 的值为
的值为
 的焦点为顶点,顶点为焦点的椭圆的标准方程是
的焦点为顶点,顶点为焦点的椭圆的标准方程是



 :
: ,命题
,命题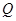 :
: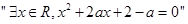 ;
; 的取值范围。
的取值范围。 的左焦点为
的左焦点为 ,过点
,过点 ,
, 两点.当直线
两点.当直线 经过椭圆的一个顶点时,其倾斜角恰为
经过椭圆的一个顶点时,其倾斜角恰为 .
.
 ,
, 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 的面积为
的面积为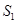 ,△
,△ (
( 为原点)的面积为
为原点)的面积为 ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号