下列说法:
① “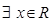 ,使
,使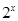 >3”的否定是“
>3”的否定是“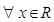 ,使
,使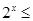 3”;
3”;
② 函数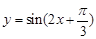 的最小正周期是
的最小正周期是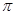 ;
;
③ “在 中,若
中,若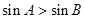 ,则
,则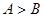 ”的逆命题是真命题;
”的逆命题是真命题;
④ “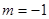 ”是“直线
”是“直线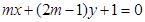 和直线
和直线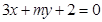 垂直”的充要条件;其中正确的说法是 (只填序号).
垂直”的充要条件;其中正确的说法是 (只填序号).
已知命题 “存在
“存在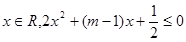 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在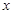 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求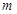 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
给出以下四个命题,所有真命题的序号为________.
①从总体中抽取样本(x1,y1),(x2,y2),…,(xn,yn),若记 ,
,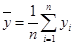 ,则回归直线y=bx+a必过点(
,则回归直线y=bx+a必过点( ,
, 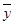 ).
).
②将函数y=cos 2x的图象向右平移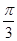 个单位,得到函数y=sin
个单位,得到函数y=sin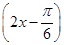 的图象;
的图象;
③已知数列{an},那么“对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件.
④命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”.
下列四个命题中,正确的有
①两个变量间的相关系数 越小,说明两变量间的线性相关程度越低;
越小,说明两变量间的线性相关程度越低;
②命题 :“
:“ ,
, ”的否定
”的否定 :“
:“ ,
, ”;
”;
③用相关指数 来刻画回归效果,若
来刻画回归效果,若 越大,则说明模型的拟合效果越好;
越大,则说明模型的拟合效果越好;
④若 ,
, ,
, ,则
,则 .
.
| A.①③④ | B.①④ | C.③④ | D.②③ |
下列说法:(1)命题“ ”的否定是“
”的否定是“ ”;
”;
(2)关于 的不等式
的不等式 恒成立,则
恒成立,则 的取值范围是
的取值范围是 ;
;
(3)对于函数 ,则有当
,则有当 时,
时, ,使得函数
,使得函数  在
在 上有三个零点;
上有三个零点;
(4)
(5)已知 ,且
,且 是常数,又
是常数,又 的最小值是
的最小值是 ,则
,则 7.其中正确的个数是 .
7.其中正确的个数是 .
下面给出四个命题:
(1) 对于实数m和向量a、b恒有:m(a – b) =" ma" – mb;
(2) 对于实数m,n和向量a,恒有:(m – n)a =" ma" – na;
(3) 若ma =" mb" (m∈R,m¹0 ), 则a = b;
(4) 若ma =" na" (m,n∈R,a ≠ 0), 则m = n.
其中正确命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
在下列给出的命题中,所有正确命题的序号为 .
①函数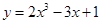 的图象关于点
的图象关于点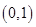 成中心对称;
成中心对称;
②对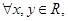 若
若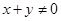 ,则
,则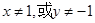 ;
;
③若实数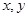 满足
满足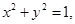 则
则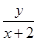 的最大值为
的最大值为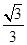 ;
;
④若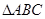 为钝角三角形,则
为钝角三角形,则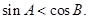
已知命题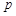 :函数
:函数 的图象恒过定点
的图象恒过定点 ;命题
;命题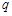 :若函数
:若函数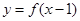 为偶函数,则函数
为偶函数,则函数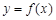 的图象关于直线
的图象关于直线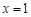 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )
A. |
B.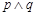 |
C.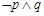 |
D. |
(1)已知命题 和命题
和命题 ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围.
的取值范围.
(2)已知命题 方程
方程 的一根在
的一根在 内,另一根在
内,另一根在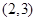 内.
内.
命题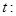 函数
函数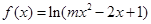 的定义域为全体实数.
的定义域为全体实数.
若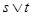 为真命题,求实数
为真命题,求实数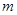 的取值范围.
的取值范围.
已知函数 的定义域为
的定义域为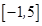 ,部分对应值如下表,
,部分对应值如下表, 的导函数
的导函数 的图象如图所示.下列关于
的图象如图所示.下列关于 的命题:
的命题:
 |
 |
0 |
4 |
5 |
 |
1 |
2 |
2 |
1 |
①函数 的极大值点为
的极大值点为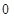 ,
, ;
;
②函数 在
在 上是减函数;
上是减函数;
③如果当 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;
④当 时,函数
时,函数 有
有 个零点。
个零点。
其中正确命题的个数有 个.