下列命题中正确的命题是:
A.若 , , ,则 ,则 ( ( ) ) |
B.若数列 , , 的极限都不存在,则 的极限都不存在,则 的极限也不存在 的极限也不存在 |
C.若数列 , , 的极限都存在,则 的极限都存在,则 的极限也存在 的极限也存在 |
D.设 ,若数列 ,若数列 的极限存在,则数列 的极限存在,则数列 的极限也存在 的极限也存在 |
下列说法正确的是( )
A.命题“若 , 则 , 则  ”的逆否命题是“若 ”的逆否命题是“若 , 则 , 则 或 或 ”; ”; |
B.命题“ , ,  ”的否定是“ ”的否定是“ , ,  ”; ”; |
C.“ ”是“函数 ”是“函数 在区间 在区间 上单调递减”的充要条件; 上单调递减”的充要条件; |
D.已知命题 ;命题 ;命题 , 则 “ , 则 “ 为真命题” 为真命题” |
给出如下三个命题:
①设a,b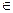 R,且
R,且 >1,则
>1,则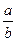 <1;
<1;
②四个非零实数a、b、c、d依次成等比数列的充要条件是ad=bc;
③若f(x)=logix,则f(|x|)是偶函数.
其中正确命题的序号是
| A.①② | B.②③ | C.①③ | D.①②③ |
某医疗研究所为了检验某种血清预防感冒的作用,把 名使用血清的人与另外
名使用血清的人与另外 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设 :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用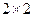 列联表计算得
列联表计算得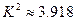 ,经查对临界值表知
,经查对临界值表知 .
.
对此,四名同学做出了以下的判断:
p:有 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用”
q:若某人未使用该血清,那么他在一年中有 的可能性得感冒
的可能性得感冒
r:这种血清预防感冒的有效率为
s:这种血清预防感冒的有效率为
则下列结论中,正确结论的序号是 .(把你认为正确的命题序号都填上)
(1) p∧﹁q; (2)﹁p∧q ;
(3)(﹁p∧﹁q)∧(r∨s); (4)(p∨﹁r)∧(﹁q∨s)
设非空集合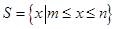 满足:当
满足:当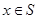 时,有
时,有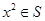 ,给出如下三个命题:
,给出如下三个命题:
①若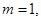 则
则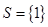 ;②若
;②若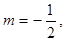 则
则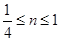 ; ③若
; ③若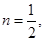 则
则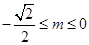 .
.
其中正确命题的是( )
| A.① | B.①② | C.②③ | D.①②③ |
已知命题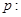 “方程
“方程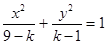 表示焦点在
表示焦点在 轴上的椭圆”,
轴上的椭圆”,
命题 “方程
“方程 表示双曲线”.
表示双曲线”.
(1)若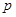 是真命题,求实数
是真命题,求实数 的取值范围;
的取值范围;
(2)若 是真命题,求实数
是真命题,求实数 的取值范围;
的取值范围;
(3)若“ ”是真命题,求实数
”是真命题,求实数 的取值范围.
的取值范围.
对于定义域为[0,1]的函数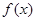 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:
①对任意的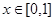 ,总有
,总有
②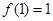
③若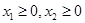 ,
, ,都有
,都有 成立;
成立;
则称函数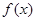 为理想函数. 下面有三个命题:
为理想函数. 下面有三个命题:
若函数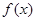 为理想函数,则
为理想函数,则 ;
;
函数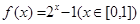 是理想函数;
是理想函数;
若函数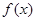 是理想函数,假定存在
是理想函数,假定存在 ,使得
,使得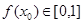 ,且
,且 ,则
,则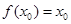 ;
;
其中正确的命题个数有( )
| A.3个 | B.2个 | C.1个 | D.0个 |
已知命题p: 方程 有两个大于-1的实数根,已知命题q:关于x的不等式
有两个大于-1的实数根,已知命题q:关于x的不等式 的解集是R,若“p或q”与“
的解集是R,若“p或q”与“ ” 同时为真命题,求实数a的取值范围(12分)
” 同时为真命题,求实数a的取值范围(12分)