高中数学截面及其作法试题

已知直线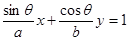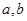：（为给定的正常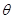数，为参数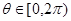，）构成的集合为S,给出下列命题： 
①当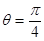时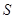，中直线的斜率为；
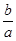②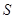中的所有直线可覆盖整个坐标平面．
③当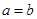时，存在某个定点，该定点到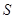中的所有直线的距离均相等；
④当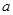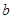＞时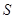，中的两条平行直线间的距离的最小值为；
其中正确的是         （写出所有正确命题的编号）．

已知命题p：函数f(x)＝x²＋ax－2在[－1,1]内有且仅有一个零点．命题q：x²＋3(a＋1)x＋2≤0在区间[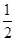，]内恒成立．若命题“p且q”是假命题，求实数a的取值范围．

下列说法正确的是（  ）

A．命题“若，则”的逆命题是“若，则”

B．命题“若，则”的否命题是“若，则”

C．已知，命题“若，则”的逆否命题是真命题

D．若，则“”是“”的充分条件

已知下列三个命题：
①棱长为2的正方体外接球的体积为4；
②如果将一组数据中的每一个数都加上同一个非零常数，那么这组数据的平均数和方差都改变；
③直线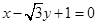被圆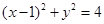截得的弦长为2．
其中真命题的序号是(  )。

A．①②

B．②③

C．①③

D．①②③

设：，：关于的不等式的解集是空集，试确定实数的取值范围，使得或为真命题，且为假命题。

设命题函数的定义域为R，命题不等式对一切正实数x均成立，如果命题为真，为假，求实数a的取值范围.

下列命题中是假命题的是(     )

A．上递减

B．

C．

D．都不是偶函数

已知命题p:.若命题p
且q是真命题,则实数a的取值范围为 (  )

A．

B．a≤-2或1≤a≤2

C．a≥1

D．-2≤a≤1

给出下列四个命题：
①命题“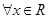，”的否定是“，”；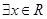
②已知回归直线的斜率的估计值是1.23，样本点的中心为（4，5），则回归直线的方程是；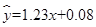
③圆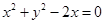的圆心到直线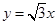的距离是；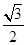
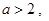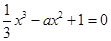④若则方程在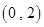上恰好有1个根；
⑤对于大于1的自然数m的二次幂可以用技术进行以下方式的“分裂”：……仿此，若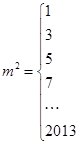，则m=1007；
其中真命题的序号是                 .（填上所有真命题的序号）

给出下列四个命题：
①命题“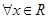，”的否定是“，”；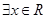
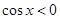②若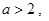则方程在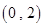上恰好有1个根；
③如果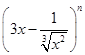的展开式中二项式系数之和为128，则展开式中的系数是；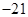
④由直线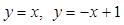，及x轴围成平面图形的面积为；
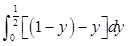其中真命题的序号是                 .（填上所有真命题的序号）

给出下列四个命题， 其中正确的命题有 个．  
（1）函数上的单调递增区间是；
（2）均为非零实数，集合，则“”是“”的必要不充分条件
（3）若为真命题，则也为真命题
（4） 命题的否定

A．

B．

C．

D．

若命题“$x∈R,x²＋ax＋1＜0”是真命题，则实数a的取值范围为  。

下列说法：
①“∃x∈R,2^x＞3”的否定是“∀x∈R,2^x≤3”；
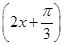②函数y＝sin sin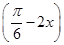的最小正周期是π；
③命题“函数f(x)在x＝x₀处有极值，则f′(x₀)＝0”的否命题是真命题；
④f(x)是(－∞，0)∪(0，＋∞)上的奇函数，x＞0时的解析式是f(x)＝2^x，则x＜0时的解析式为f(x)＝－2^－x.其中正确的说法是________．

下列说法中正确的是 （   ）

A．“”是“函数是奇函数”的充要条件；

B．若．则；

C．若为假命题，则均为假命题；

D．“若，则”的否命题是“若，则”．

命题： ；命题：解集非空．
若，求的取值范围．