[江西]2013-2014学年江西赣州六校高二上学期期末联考理科数学试卷
下列说法中,正确的是:( )
A.命题“若 ,则 ,则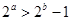 ”的否命题为“若 ”的否命题为“若 ,则 ,则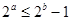 ” ” |
B.命题“存在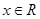 ,使得 ,使得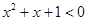 ”的否定是:“任意 ”的否定是:“任意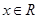 ,都有 ,都有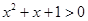 ” ” |
C.若命题“非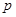 ”与命题“ ”与命题“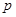 或 或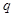 ”都是真命题,那么命题 ”都是真命题,那么命题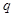 一定是真命题 一定是真命题 |
D.命题“若 ,则 ,则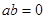 ”的逆命题是真命题 ”的逆命题是真命题 |
从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为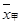 ,
, ,方差分别为
,方差分别为 ,
, ,则( )
,则( )
A.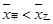 , ,   |
B.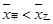 , , 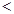  |
C. , ,   |
D. , , 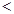  |
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
(1)若 ,则
,则 ;
;
(2)若

 ,
,

 ,
, ,则
,则 ;
;
(3)若 ,
,

 ,则
,则 ;
;
(4)若 ,
, ,
, ,
, ,则
,则 .
.
其中正确的命题是( )
| A.(1)(3) | B.(2)(3) |
| C.(2)(4) | D.(3)(4) |
已知椭圆 和双曲线
和双曲线 有相同的焦点
有相同的焦点 ,
, 是两曲线的一个交点,则
是两曲线的一个交点,则 的值是( )
的值是( )
A. |
B. |
C. |
D. |
给出右图所示的算法流程图,若输出的值为 ,则判断框中的条件是( )
,则判断框中的条件是( )
A. |
B. |
C. |
D. |
如图,设四面体 各棱长均相等,
各棱长均相等, 分别为
分别为 中点,则
中点,则 在该四面体的面
在该四面体的面 上的射影是下图中的( )
上的射影是下图中的( )




A. B. C. D.
“过点 的直线
的直线 与双曲线
与双曲线 有且仅有一个公共点”是“直线
有且仅有一个公共点”是“直线 的斜率
的斜率 的值为
的值为 ”的( )
”的( )
| A.充分必要条件 | B.充分但不必要条件 |
| C.必要但不充分条件 | D.既不充分也不必要条件 |
如图所示 方格,在每一个方格中填入一个数字,数字可以是
方格,在每一个方格中填入一个数字,数字可以是 中的任何一个,允许重复,则填入
中的任何一个,允许重复,则填入 方格的数字大于
方格的数字大于 方格的数字的概率为( )
方格的数字的概率为( )
A. |
B. |
C. |
D. |
如图,在棱长为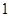 的正方体
的正方体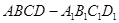 的对角线
的对角线 上任取一点
上任取一点 ,以
,以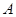 为球心,
为球心,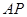 为半径作一个球.设
为半径作一个球.设 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为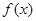 ,则函数
,则函数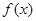 的图象最有可能的是( )
的图象最有可能的是( )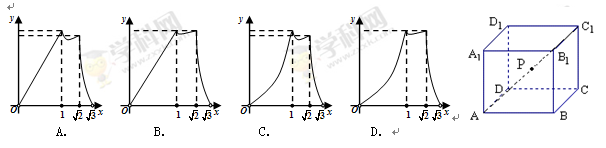
某校为了了解高三学生的身体状况,抽取了 名女生,测量其体重.将所得的数据整理后,画出了如图所示的频率分布直方图,则所抽取的女生中体重在
名女生,测量其体重.将所得的数据整理后,画出了如图所示的频率分布直方图,则所抽取的女生中体重在 的人数是
的人数是 
如图,在长方形 中,
中, 为
为 的中点,
的中点, 为线段
为线段 (端点除外)上一动点,现将
(端点除外)上一动点,现将 沿
沿 折起,使平面
折起,使平面 平面
平面 .在平面
.在平面 内过点
内过点 作
作 为垂足,设
为垂足,设 ,则
,则 的取值范围是________
的取值范围是________
已知 ,直线
,直线 和曲线
和曲线 有两个不同的交点,他们围成的平面区域为
有两个不同的交点,他们围成的平面区域为 ,向区域
,向区域 上随机投以点
上随机投以点 ,点
,点 落在
落在 内的概率为
内的概率为 ,若
,若 ,则实数
,则实数 的取值范围是:
的取值范围是:
已知离心率为 的椭圆
的椭圆 (
( )过点
)过点
(1)求椭圆 的方程;
的方程;
(2)过点 作斜率为
作斜率为 直线
直线 与椭圆相交于
与椭圆相交于 两点,求
两点,求 的长.
的长.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、 人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求 的值;
的值;
(2)把在前排就坐的高二代表队6人分别记为 ,现随机从中抽取2人上台抽奖,
,现随机从中抽取2人上台抽奖,
求 和
和 至少有一人上台抽奖的概率;
至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个 之间的均匀随机数
之间的均匀随机数 ,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
,并按如右所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
已知命题 “存在
“存在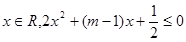 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在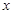 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”
表示双曲线”
(1)若“ 且
且 ”是真命题,求
”是真命题,求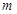 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围。
的取值范围。
如图,已知四棱锥 中,底面
中,底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明: 平面
平面 ;
;
(2)取 ,若
,若 为
为 上的动点,
上的动点, 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值。
的余弦值。
 的焦点坐标为( )
的焦点坐标为( )



 且
且 ,则
,则
 与椭圆
与椭圆 相交于
相交于 两点,且线段
两点,且线段 的中点在直线
的中点在直线 上,则此椭圆的离心率为_______
上,则此椭圆的离心率为_______ 中,
中, 分别是
分别是 的中点.
的中点.
 平面
平面 ;
; 的体积.
的体积. 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切. ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 ,线段
,线段 垂直平分线交
垂直平分线交 ,求点
,求点 的方程;
的方程; 轴交于点
轴交于点 ,不同的两点
,不同的两点 在
在 ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号