浙江省杭州市高三第二次模拟数学(文)卷
函数 ,
, 是
是
A.最小正周期为 的偶函数 的偶函数 |
B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 |
D.最小正周期为 的奇函数 的奇函数 |
已知| a | =" |" b | =" 2," a·b =" -2," 且(a + b)⊥(a +  b), 则实数
b), 则实数 的值为
的值为
| A.–1 | B.1 | C.–2 | D.2 |
若 是两个相交平面, 点
是两个相交平面, 点 不在
不在 内, 也不在
内, 也不在 内, 则过点
内, 则过点 且与
且与 和
和 都平行的直线
都平行的直线
| A.只有1条 | B.只有2条 | C.只有4条 | D.有无数条 |
停车场可把12辆车停放在一排上, 当有8辆车已停放后, 而恰有4个空位在一起, 这样的事件发生的概率是
A. |
B. |
C. |
D. |
对于二项式
 , 有四个判断: ① 存在
, 有四个判断: ① 存在 , 展开式中有常数项; ② 对任意
, 展开式中有常数项; ② 对任意 , 展开式中没有常数项; ③ 对任意
, 展开式中没有常数项; ③ 对任意 , 展开式中没有
, 展开式中没有 的一次项; ④ 存在
的一次项; ④ 存在 , 展开式中有
, 展开式中有 的一次项. 上述判断中正确的是
的一次项. 上述判断中正确的是
| A.①与③ | B.②与③ | C.②与④ | D.①与④ |
给出平面区域 , 如图所示, 其中
, 如图所示, 其中
 . 若使目标函数
. 若使目标函数 取得最大值的最优解有无穷多个, 则
取得最大值的最优解有无穷多个, 则 的值为
的值为
| A.4 | B.2 | C. |
D. |
已知函数 , 函数
, 函数 定义如下: 当
定义如下: 当 时,
时,  ; 当
; 当 时,
时,  .
.
那么
有最小值0, 无最大值 (B) 有最小值-1, 无最大值
(C) 有最大值1, 无最小值 (D) 无最小值, 也无最大值
正方形 的边长是2,
的边长是2,  分别是
分别是 和
和 的中点, 将正方形沿
的中点, 将正方形沿 折成直二面角(如图所示).
折成直二面角(如图所示).  为矩形
为矩形 内一点, 如果
内一点, 如果
 和平面
和平面 所成角的正切值为
所成角的正切值为 ,那么点
,那么点 到直线
到直线 的距离为 _______
的距离为 _______
某健康中心研究认为:身高为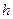 (cm)的人的其理想体重
(cm)的人的其理想体重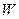 (kg),应符合公式
(kg),应符合公式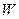 =22
=22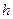 2 (kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高
2 (kg),且定义体重在理想体重±10%的范围内,称为标准体重;超过10%但不超过20%者,称为微胖;超过20%者,称为肥胖, 微胖及肥胖都是过重的现象. 对身高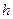 ,体重
,体重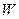 的人,体重过重的充要条件为
的人,体重过重的充要条件为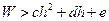 ,则
,则 __________
__________
(本小题满分14分)
已知数列{ }是首项为
}是首项为 等于1且公比
等于1且公比 不等于1的等比数列,
不等于1的等比数列, 是其前
是其前 项的和,
项的和, 成等差数列.
成等差数列.
(1) 求和  ;
;
(2) 证明 12 成等比数列
成等比数列
(本小题满分14分)
设甲、已、丙三人每次射击命中目标的概率分别为0.7、0.6和0.5.
三人各向目标射击一次,求至少有一人命中目标的概率;
三人各向目标射击一次,求恰有两人命中目标的概率;
(3)若甲单独向目标射击三次,求他恰好命中两次的概率.
(本小题满分14分)
如图, 在四棱锥 中,顶点
中,顶点 在底面
在底面 上的射影恰好落在
上的射影恰好落在 的中点
的中点 上,又∠
上,又∠ ,
, ,且
,且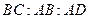
=1:2:2.
(1) 求证: 
(2) 若 , 求直线
, 求直线 与
与 所成的角的余弦值;
所成的角的余弦值;
(3) 若平面 与平面
与平面 所成的角为
所成的角为 , 求
, 求 的值
的值
(本小题满分14分)
已知奇函数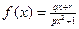 有最大值
有最大值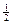 , 且
, 且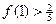 , 其中实数
, 其中实数 是正整数.
是正整数.
求 的解析式;
的解析式;
令 , 证明
, 证明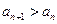 (
( 是正整数).
是正整数).
 , 则满足
, 则满足 的集合
的集合 的个数是
的个数是 的准线与
的准线与 轴平行, 那么
轴平行, 那么 的取值范围为
的取值范围为



 射到直线
射到直线 上, 被
上, 被



 上, 且过点
上, 且过点 的圆的方程是 ______
的圆的方程是 ______
 的值
的值 的值
的值 的对称轴上任一点
的对称轴上任一点 作直线与抛物线交于
作直线与抛物线交于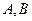 两点,点
两点,点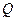 是点
是点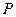 关于原点的对称点.
关于原点的对称点.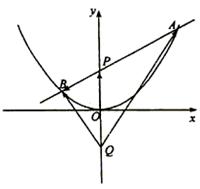
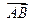 所成的比为
所成的比为 ,证明:
,证明:
 ;
; 的方程是
的方程是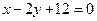 ,过
,过 与抛物线在点
与抛物线在点 处有共同的切线,求圆
处有共同的切线,求圆 粤公网安备 44130202000953号
粤公网安备 44130202000953号