、对于函数 与函数
与函数 有下列命题:
有下列命题:
①无论函数 的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
的图像通过怎样的平移所得的图像对应的函数都不会是奇函数;
②函数 的图像与两坐标轴及其直线
的图像与两坐标轴及其直线 所围成的封闭图形的面积为4;
所围成的封闭图形的面积为4;
③方程 有两个根;
有两个根;
④函数 图像上存在一点处的切线斜率小于0;
图像上存在一点处的切线斜率小于0;
⑤若函数 在点P处的切线平行于函数
在点P处的切线平行于函数 在点Q处的切线,则直线PQ的斜率为
在点Q处的切线,则直线PQ的斜率为 ,其中正确的命题是________.(把所有正确命题的序号都填上)
,其中正确的命题是________.(把所有正确命题的序号都填上)
下列结论错误的是________.
①命题“若p,则q”与命题“若綈q,则綈p”互为逆否命题;
②命题p:∀x∈[0,1],ex≥1,命题q:∃x∈R,x2+x+1<0,则p∨q为真;
③“若am2<bm2,则a<b”的逆命题为真命题;
④若p∨q为假命题,则p、q均为假命题.
下列四种说法:
①命题“ ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”;
②设 、
、 是简单命题,若“
是简单命题,若“ ”为假命题,则“
”为假命题,则“ ” 为真命题;
” 为真命题;
③若 是
是 的充分不必要条件,则
的充分不必要条件,则 的必要不充分条件;
的必要不充分条件;
④把函数
 的图像上所有的点向右平移
的图像上所有的点向右平移 个单位即可得到函数
个单位即可得到函数
 的图像.
的图像.
其中所有正确说法的序号是 .
.下列5个命题:
(1)函数 的图象向左平移
的图象向左平移 个单位,所得函数图象关于原点对称;
个单位,所得函数图象关于原点对称;
(2)若命题p:“存在 ”,则命题p的否定为:“任意
”,则命题p的否定为:“任意 ”;
”;
(3)函数 的零点有2个;
的零点有2个;
(4)函数 在
在 处取最小值;
处取最小值;
(5) 已知直线 与圆
与圆 交于不同两点A、B,O为坐标原点,则“
交于不同两点A、B,O为坐标原点,则“ ”是“向量
”是“向量 满足
满足 ”的充分不必要条件.
”的充分不必要条件.
其中所有正确命题的序号是________.
给出下列命题:
⑴函数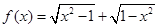 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
⑵在△ 中,若
中,若 ,则
,则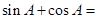
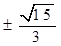 ;
;
⑶若角的集合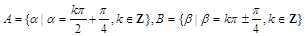 ,则
,则 ;
;
⑷设函数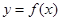 定义域为R,且
定义域为R,且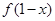 =
=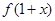 ,则
,则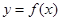 的图象关于
的图象关于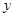 轴对称;
轴对称;
⑸函数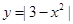 的图象和直线
的图象和直线 的公共点不可能是1个.
的公共点不可能是1个.
其中正确的命题的序号是
给出下列命题:
(1)设 是两个单位向量,它们的夹角是
是两个单位向量,它们的夹角是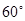 ,则
,则
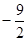 ;
;
(2)已知函数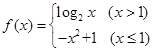 ,若函数
,若函数 有3个零点,则0<
有3个零点,则0< <1;
<1;
(3)已知函数 的定义域和值域都是
的定义域和值域都是 ,则
,则 =1;
=1;
(4)定义在R上的函数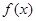 满足
满足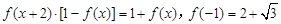 ,则
,则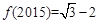 .
.
其中,正确命题的序号为 .
给出如下四个命题:①若“ 或
或 ”为真命题,则
”为真命题,则 、
、 均为真命题;
均为真命题;
②命题“若 且
且 ,则
,则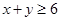 ”的否命题为“若
”的否命题为“若 且
且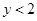 ,则
,则 ”;
”;
③在 中,“
中,“ ”是“
”是“ ”的充要条件.
”的充要条件.
④命题 “ ”是真命题.其中正确的命题的个数是 .
”是真命题.其中正确的命题的个数是 .
下列命题中,真命题的是 .
①必然事件的概率等于l
②命题“若b=3,则b2=9”的逆命题
③对立事件一定是互斥事件
④命题“相似三角形的对应角相等”的逆否命题
给出下列四个命题:
①“向量 ,
, 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“ ·
· >0”;
>0”;
②如果f(x)=lgx,则对任意的x1、x2Î(0,+¥),且x1¹x2,都有f( )>
)> ;
;
③设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意xÎ[a,b],都有|f(x)?g(x)|£1成立,则称f(x)和g(x)在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若f(x)=x2?3x+4与g(x)=2x?3在[a,b]上是“密切函数”,则其“密切区间”可以是[2,3];
④记函数y=f(x)的反函数为y=f?1(x),要得到y=f?1(1?x)的图象,可以先将y=f(x)的图象关于直线y=x做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到y=f?1(1?x)的图象.其中真命题的序号是 。(请写出所有真命题的序号)
某医疗研究所为了了解某种血清预防感冒的作用,把500名使用过该血清的人与另外500名未使用该血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”.已知利用2×2列联表计算得K2≈3.918,经查临界值表知P(K2≥3.841)≈0.05.则下列结论中,正确结论的序号是________.
①有95%的把握认为“这种血清能起到预防感冒的作用”;②若某人未使用该血清,那么他在一年中有95%的可能性得感冒;③这种血清预防感冒的有效率为95%;④这种血清预防感冒的有效率为5%.