已知函数 (
( ),将
),将 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数 的图象,函数
的图象,函数 与函数
与函数 的图象关于直线
的图象关于直线 对称.
对称.
(1)求函数 和
和 的解析式;
的解析式;
(2)若方程 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求 的取值范围;
的取值范围;
(3)设 ,已知
,已知 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(本小题13分)已知函数 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)若对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数 的最小值;
的最小值;
(2)若过点 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.
甲、乙两人在一次赛跑中,从同一地点出发,路程S与时间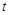 的函数关系如图所示,则下列说法正确的是
的函数关系如图所示,则下列说法正确的是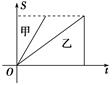
| A.甲比乙先出发 | B.乙比甲跑的路程多 |
| C.甲、乙两人的速度相同 | D.甲比乙先到达终点 |
设函数f(x)= (x∈Z).给出以下三个判断:①f(x)为偶函数;②f(x)为周期函数;③f(x+1)+ f(x)=1.其中正确判断的序号是________(填写所有正确判断的序号).
(x∈Z).给出以下三个判断:①f(x)为偶函数;②f(x)为周期函数;③f(x+1)+ f(x)=1.其中正确判断的序号是________(填写所有正确判断的序号).
已知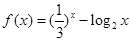 ,实数
,实数 、
、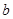 、
、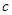 满足
满足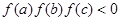 ,
,
且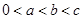 ,若实数
,若实数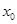 是函数
是函数 的一个零点,那么下列不等式中,不可能成立的( )
的一个零点,那么下列不等式中,不可能成立的( )
A.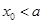 |
B.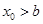 |
C. |
D.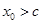 |