高中数学三面角、直三面角的基本性质试题

已知定义在上的两个函数：，在的值域为，若对任意的，总存在，使得=成
立，则实数的取值范围是           .

定义在 $R$上的函数 $f\left(x\right)$满足 $f(x+1)2f\left(x\right)$.若当 $0\le x\le 1$时。 $f\left(x\right)=x(1-x)$，则当 $-1\le x\le 0$时， $f\left(x\right)$=.

已知函数，则的值是  

A．

B．

C．

D．

 函数在上为减函数，则实数的取值范围是

A．

B．

C．

D．

设 $S,T$是R的两个非空子集，如果存在一个从 $S$到 $T$的函数 $y=f\left(x\right)$,（i） $T=\left\{f\left(x\right)|x\in S\right\}$（ii）对任意 $x_1,x_2\in S$,当 $x_1<x_2$时，恒有 $f\left(x_1\right)<f\left(x_2\right)$.那么称这两个集合"保序同构"，现给出以下3对集合：

① $A=N,B=N^{*}$&#xa0; &#xa0;② $A=\left\{x|-1\le \le 3\right\},B=\left\{x|-8\le x\le 10\right\}$&#xa0;&#xa0;③ $A=\left\{x|0\le x\le 1\right\},B=R$

其中，"保序同构"的集合对的序号是.（写出"保序同构"的集合对的序号）.

函数f(x)＝log2  (x>2)的最小值是(　　)

A．1	B．2
C．3	D．4

函数在定义域R内可导，若，且当时，，设a=f(0).b=则   （    ）

A．a<b<c

B．c<b<a

C．c<a<b

D．b<c<a

已知函数（），正项等比数列满足，则

A．99

B．

C．

D．

已知函数，
（1）若，求的范围；   （2）不等式对任意恒成立，求实数的取值范围。

下列说法中：
①指数函数的定义域为；②函数与函数互为反函数；
③空集是任何一个集合的真子集；④若（为常数），则函数的最大值为；⑤函数的值域为．
正确的是          　　 　　　（请写出所有正确命题的序号）．

定义在上的函数，当时，，且对任意的满足
（常数），则函数在区间上的最小值是（   ）

A．

B．

C．

D．

函数的值域是       ．

若函数的定义域都是R，则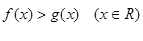成立的充要条件是（   ）

A．有一个，使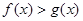	B．有无数多个，使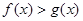
C．对R中任意的x，使	D．在R中不存在x，使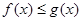

(1)化简；
(2)已知且，求的值.

已知，若满足，
（1）求实数的值；       （2）判断函数的单调性，并加以证明。