甲、乙两人在一次赛跑中,从同一地点出发,路程S与时间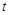 的函数关系如图所示,则下列说法正确的是
的函数关系如图所示,则下列说法正确的是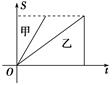
| A.甲比乙先出发 | B.乙比甲跑的路程多 |
| C.甲、乙两人的速度相同 | D.甲比乙先到达终点 |
设函数f(x)= (x∈Z).给出以下三个判断:①f(x)为偶函数;②f(x)为周期函数;③f(x+1)+ f(x)=1.其中正确判断的序号是________(填写所有正确判断的序号).
(x∈Z).给出以下三个判断:①f(x)为偶函数;②f(x)为周期函数;③f(x+1)+ f(x)=1.其中正确判断的序号是________(填写所有正确判断的序号).
已知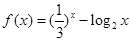 ,实数
,实数 、
、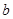 、
、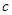 满足
满足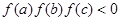 ,
,
且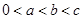 ,若实数
,若实数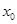 是函数
是函数 的一个零点,那么下列不等式中,不可能成立的( )
的一个零点,那么下列不等式中,不可能成立的( )
A.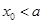 |
B.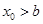 |
C. |
D.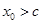 |
为了在夏季降温和冬季供暖时减少能源损耗,房屋的房顶和外墙需要建造隔热层,某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用为C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= (0
(0 x
x 10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
10),若不建隔热层,每年能源消耗费用为8万元。设f(x)为隔热层建造费用与20年的能源消耗费用之和。
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值。
已知函数 在
在 是增函数,
是增函数, 在(0,1)为减函数.
在(0,1)为减函数.
(I)求 、
、 的表达式;
的表达式;
(II)求证:当 时,方程
时,方程 有唯一解;
有唯一解;
(Ⅲ)当 时,若
时,若 在
在 ∈
∈ 内恒成立,求
内恒成立,求 的取值范围.
的取值范围.
(14分)已知函数 的图象过原点,且关于点(-1,1)成中心对称.(1)求函数
的图象过原点,且关于点(-1,1)成中心对称.(1)求函数 的解析式;(2) 若数列
的解析式;(2) 若数列 (nÎN*)满足:
(nÎN*)满足: ,求数列
,求数列 的通项公式
的通项公式 .
.
若函数 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知某公司生产某品牌服装的年固定成本为10万元,每生产千件需另投入2.7万元,设该公司年内共生产该品牌服装千件并全部销售完,每千件的销售收入为 万元,且
万元,且 .
.
(1)写出年利润 (万元)关于年产品(千件)的函数解析式;
(万元)关于年产品(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
(注:年利润=年销售收入-年总成本)
(本小题满分12分)
学校要建一个面积为392 m2的长方形游泳池,并且在四周要修建出宽为2m和4 m的小路(如图所示)。
问游泳池的长和宽分别为多少米时,占地面积最小?并求出占地面积的最小值。
设定义在 上的函数
上的函数 是最小正周期为
是最小正周期为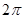 的偶函数,当
的偶函数,当 时,
时, ,且在
,且在 上单调递减,在
上单调递减,在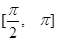 上单调递增,则函数
上单调递增,则函数 在
在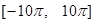 上的零点个数为 .
上的零点个数为 .
设函数 ,且
,且 ,
, ,求证:(1)
,求证:(1) 且
且 ;
;
(2)函数 在区间
在区间 内至少有一个零点;
内至少有一个零点;
(3)设 是函数
是函数 的两个零点,则
的两个零点,则 .
.