[江苏]2013届江苏省如东县高三12月四校联考文科数学试卷
(本题满分16分)
如图,开发商欲对边长为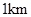 的正方形
的正方形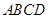 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路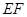 (点
(点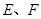 分别在
分别在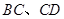 上),根据规划要求
上),根据规划要求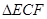 的周长为
的周长为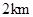 .
.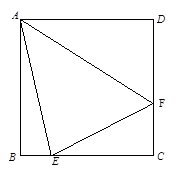
(1)设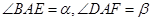 ,求证:
,求证: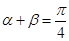 ;
;
(2)欲使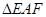 的面积最小,试确定点
的面积最小,试确定点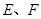 的位置.
的位置.
(本小题满分16分)
已知椭圆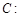
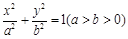 的离心率为
的离心率为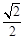 ,一条准线
,一条准线 .
.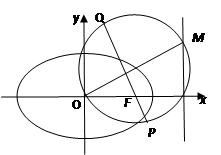
(1)求椭圆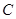 的方程;
的方程;
(2)设O为坐标原点,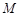 是
是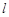 上的点,
上的点,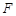 为椭圆
为椭圆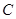 的右焦点,过点F作OM的垂线与以OM为直径的圆
的右焦点,过点F作OM的垂线与以OM为直径的圆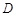 交于
交于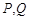 两点.
两点.
①若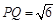 ,求圆
,求圆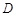 的方程;
的方程;
②若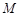 是l上的动点,求证:点
是l上的动点,求证:点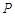 在定圆上,并求该定圆的方程.
在定圆上,并求该定圆的方程.
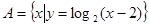 ,
,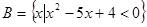 ,则
,则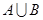 = .
= .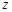 满足
满足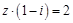 ,其中
,其中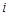 为虚数单位,则
为虚数单位,则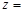 .
.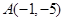 和向量
和向量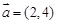 ,若
,若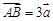 ,则点B的坐标为 .
,则点B的坐标为 .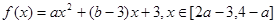 是偶函数,则
是偶函数,则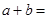 .
.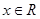 ,那么
,那么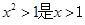 的 条件(“充要”,“充分不必要”,“必要不充分” “既不充分又不必要”)
的 条件(“充要”,“充分不必要”,“必要不充分” “既不充分又不必要”)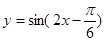 的图象,可以将函数
的图象,可以将函数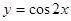 的图象向右平移 ______个单位长度
的图象向右平移 ______个单位长度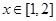 满足
满足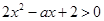 ,则实数
,则实数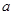 的取值范围是 .
的取值范围是 .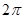 的半圆面,则该圆锥的体积为 .
的半圆面,则该圆锥的体积为 .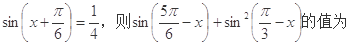 .
. 为
为 中的最小值,设
中的最小值,设 ,则
,则 的最大值是 .
的最大值是 . 中,
中,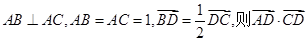 的值等于 .
的值等于 .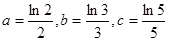 ,则a,b,c的大小关系是 .
,则a,b,c的大小关系是 .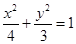 的左焦点为
的左焦点为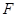 ,直线
,直线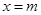 与椭圆相交于点
与椭圆相交于点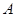 、
、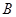 ,当
,当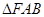 的周长最大时,
的周长最大时, 函数
函数 ,若存在
,若存在 ,使得
,使得 成立,则实数a的取值范围是 .
成立,则实数a的取值范围是 .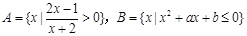 ,且
,且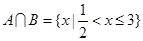 ,
,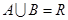 ,求:(1)
,求:(1)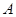 (2)实数
(2)实数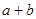 的值.
的值. 中,侧面
中,侧面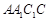
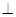 底面ABC,侧面
底面ABC,侧面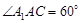 ,E、F分别是
,E、F分别是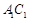 、AB的中点.
、AB的中点.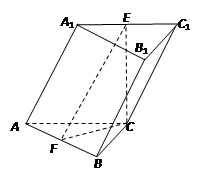
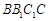 ;
;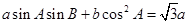 ,
,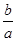 ;(2)当
;(2)当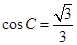 时,求
时,求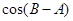 的值。
的值。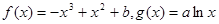 ,
,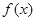 在
在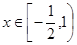 上的最大值为
上的最大值为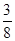 ,求实数
,求实数 的值;
的值;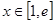 ,都有
,都有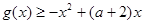 恒成立,求实数
恒成立,求实数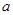 的取值范围;
的取值范围;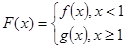 ,对任意给定的正实数
,对任意给定的正实数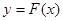 上是否存在两点
上是否存在两点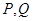 ,使得
,使得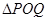 是以
是以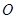 (
( 轴上?请说明理由。
轴上?请说明理由。 粤公网安备 44130202000953号
粤公网安备 44130202000953号