利民商店经销某种洗衣粉,年销售量为6000包,每包进价2.80元,销售价3.40元,全年分若干次进货,每次进货x包,已知每次进货运输劳务费62.50元,全年保管费为1.5x元。
(1)把该商店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大,每次应该进货多少包?
甲、乙两人在一次赛跑中,从同一地点出发,路程S与时间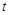 的函数关系如图所示,则下列说法正确的是
的函数关系如图所示,则下列说法正确的是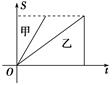
| A.甲比乙先出发 | B.乙比甲跑的路程多 |
| C.甲、乙两人的速度相同 | D.甲比乙先到达终点 |
已知函数 在
在 是增函数,
是增函数, 在(0,1)为减函数.
在(0,1)为减函数.
(I)求 、
、 的表达式;
的表达式;
(II)求证:当 时,方程
时,方程 有唯一解;
有唯一解;
(Ⅲ)当 时,若
时,若 在
在 ∈
∈ 内恒成立,求
内恒成立,求 的取值范围.
的取值范围.
若函数 在
在 上单调递增,那么实数
上单调递增,那么实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和 组成数对(
组成数对( ,并构成函数
,并构成函数
(Ⅰ)写出所有可能的数对( ,并计算
,并计算 ,且
,且 的概率;
的概率;
(Ⅱ)求函数 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.
设定义在 上的函数
上的函数 是最小正周期为
是最小正周期为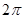 的偶函数,当
的偶函数,当 时,
时, ,且在
,且在 上单调递减,在
上单调递减,在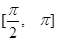 上单调递增,则函数
上单调递增,则函数 在
在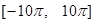 上的零点个数为 .
上的零点个数为 .
(本小题满分14分)
已知函数f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)当b=0时,若对 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线,切点分别为(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求证:x1>1>x2;
②若当x≥x1时,关于x的不等式ax2-x+xe +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围.
设函数 ,且
,且 ,
, ,求证:(1)
,求证:(1) 且
且 ;
;
(2)函数 在区间
在区间 内至少有一个零点;
内至少有一个零点;
(3)设 是函数
是函数 的两个零点,则
的两个零点,则 .
.