(本小题满分12分)已知函数 (
( 为常数)。
为常数)。
(Ⅰ)函数 的图象在点(
的图象在点( )处的切线与函数
)处的切线与函数 的图象相切,求实数
的图象相切,求实数 的值;
的值;
(Ⅱ)设 ,若函数
,若函数 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数 的取值范围;
的取值范围;
(Ⅲ)若 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数 ,
, ,都有
,都有 成立,求
成立,求 的取值范围。
的取值范围。
(本小题满分12分)
已知函数 是奇函数:
是奇函数:
(1)求实数 和
和 的值;
的值;
(2)证明 在区间
在区间 上的单调递减
上的单调递减
(3)已知 且不等式
且不等式 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设 是函数
是函数 定义域内的一个区间,若存在
定义域内的一个区间,若存在 ,使
,使 ,
,
则称 是
是 的一个“次不动点”,也称
的一个“次不动点”,也称 在区间
在区间 上存在次不动点.若函数
上存在次不动点.若函数 在区间
在区间 上存在次不动点,则实数
上存在次不动点,则实数 的取值范围
的取值范围
是 .
函数 的图像与
的图像与 轴的交点个数为 ( )
轴的交点个数为 ( )
| A.一个 | B.至少一个 | C.至多两个 | D.至多一个 |
14分)某出版社新出版一本高考复习用书,该书的成本为5元/本,经销过程中每本书需付给代理商m元(1≤m≤3)的劳务费,且出版的书可全部销售完. 经出版社研究决定,新书投放市场后定价为 元/本(9≤
元/本(9≤ ≤11),预计一年的销售量为
≤11),预计一年的销售量为 万本.
万本.
(1)求该出版社一年的利润 (万元)与每本书的定价
(万元)与每本书的定价 的函数关系式;
的函数关系式;
已知函数 (其中a,b为实常数)。
(其中a,b为实常数)。
(Ⅰ)讨论函数 的单调区间:
的单调区间:
(Ⅱ)当 时,函数
时,函数 有三个不同的零点,证明:
有三个不同的零点,证明: :
:
(Ⅲ)若 在区间
在区间 上是减函数,设关于x的方程
上是减函数,设关于x的方程 的两个非零实数根为
的两个非零实数根为 ,
, 。试问是否存在实数m,使得
。试问是否存在实数m,使得 对任意满足条件的a及t
对任意满足条件的a及t 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。
已知函数
 .
.
(1)讨论函数 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数 在
在 处取得极值,对
处取得极值,对
 ,
, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当 且
且 时,试比较
时,试比较 的大小.
的大小.
已知二次函数
(1)若 试判断函数
试判断函数 零点个数;
零点个数;
(2)若对任意的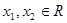 ,且
,且 <
<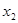 ,
,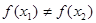 (
(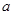 >0),试证明:
>0),试证明: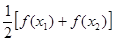 >
> 成立。
成立。
(3)是否存在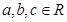 ,使
,使 同时满足以下条件:①对任意
同时满足以下条件:①对任意 ,
, ,且
,且 ②对任意的
②对任意的 ,都有
,都有 ?若存在,求出
?若存在,求出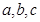 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。