(本小题满分12分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数.
的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式
的表达式
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时) 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
(本题满分16分)(Ⅰ)试比较 的大小;
的大小;
(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.
已知f(x)=-3x2+m(6-m)x+n
(1) 解关于m的不等式f(1)>0;
(2) 当不等式f(x)>0的解集为(-1,3)时,求实数m,n的值。
(本小题满分12分)已知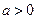 ,设命题
,设命题 函数
函数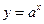 在R上单调递减,
在R上单调递减,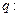 不等式
不等式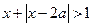 的解集为R,若
的解集为R,若 和
和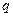 中有且只有一个命题为真命题,求
中有且只有一个命题为真命题,求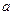 的取值范围.
的取值范围.
((本题13分)汽车和自行车分别从A地和C地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知AC=100米。(汽车开到C地即停止)
(1)经过 秒后,汽车到达B处,自行车到达D处,设B、D间距离为
秒后,汽车到达B处,自行车到达D处,设B、D间距离为 ,写出
,写出 关于
关于 的函数关系式,并求出定义域。
的函数关系式,并求出定义域。
(2)经过多少时间后,汽车和自行车之间的距离最短?最短距离是多少?
为了提高产品的年产量,某企业拟在2010年进行技术改革.经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3-(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产的产品均能销售出去.厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金).
(1)将2010年该产品的利润y万元(利润=销售金额-生产成本-技术改革费用)表示为技术改革费用m万元的函数;
(2)该企业2010年的技术改革费用投入多少万元时,厂家的利润最大?
(本题满分12分12分)设a,b∈R+,a+b=1.
(1)证明:ab+ ≥4+
≥4+ =4
=4 ;
;
(2)探索、猜想,将结果填在括号内;
a2b2+ ≥( _________ );a3b3+
≥( _________ );a3b3+ ≥( _________ );
≥( _________ );
(3)由(1)(2)你能归纳出更一般的结论吗?请证明你得出的结论.
(本小题满分13分)
为了预防甲型流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为 (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
(1)求从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过多少小时后,学生才能回到教室.
 要在墙上开一个上部为半圆,下部为矩形的窗户
要在墙上开一个上部为半圆,下部为矩形的窗户
(如图所示),在窗框总长度为 的条件下,
的条件下,
(1)请写 出窗户的面积
出窗户的面积 与圆的直径
与圆的直径 的函数关系;
的函数关系;
(2)要使窗户透光面积最大,窗户应具有怎样的尺寸?并写出最大值.
满分10分) 设有关于 的一元二次方程
的一元二次方程
(Ⅰ)若 是从
是从 四个数中任取的一个数,
四个数中任取的一个数, 是从
是从 三个数中任取的一个数,求上述方程有实根的概率
三个数中任取的一个数,求上述方程有实根的概率
(Ⅱ)若 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实根的概率
任取的一个数,求上述方程有实根的概率
(本小题满分14分)
已知函数 对一切实数x,y都有
对一切实数x,y都有 成立,且
成立,且 .
.
(1)求 的值
的值
(2)求 的解析式
的解析式
(3)若 ,对任意的
,对任意的 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围