要在墙上开一个上部为半圆，下部为矩形的窗户
（如图所示），在窗框总长度为
的条件下，
（1）请写
出窗户的面积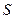
与圆的直径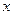
的函数关系；
（2）要使窗户透光面积最大，窗户应具有怎样的尺寸？并写出最大值.
和
的最大公约数，并用更相减损术检验所得结果.
+
+
+…+
的值的流程图.
,写出该函数的函数值的算法并画出流程图.相关知识点
推荐套卷
要在墙上开一个上部为半圆，下部为矩形的窗户
（如图所示），在窗框总长度为的条件下，
（1）请写出窗户的面积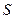与圆的直径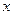的函数关系；
（2）要使窗户透光面积最大，窗户应具有怎样的尺寸？并写出最大值.
粤公网安备 44130202000953号