（本小题满分12分）如图，四棱锥P-ABCD中，PD⊥平面ABCD，PD="DC=BC=1," AB="2," AB∥DC，∠BCD=900
(1)求证：PC⊥BC
(2)求点A到平面PBC的距离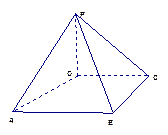
相关试题
的逆矩阵.
,计算N2.
对应的变换,再作矩阵B=
对应的变换得到曲线C2:
+y2=1,求实数b的值.
的作用下变换为曲线x2-y2=1,试求a+b的值.
.
,3)在该变换作用下的象.相关知识点
推荐套卷
（本小题满分12分）如图，四棱锥P-ABCD中，PD⊥平面ABCD，PD="DC=BC=1," AB="2," AB∥DC，∠BCD=900
(1)求证：PC⊥BC
(2)求点A到平面PBC的距离
粤公网安备 44130202000953号