高中数学三面角、直三面角的基本性质解答题

对于函数，若存在，使得成立，称为不动点，已知函数
（1） 当时，求函数不动点.
(2)若对任意的实数，函数恒有两个相异的不动点，求a的取值范围.

已知方程,求使方程有两个大于的实数根的充要条件。

某市旅游部门开发一种旅游纪念品，每件产品的成本是元，销售价是元，月平均销售件.通过改进工艺，产品的成本不变，质量和技术含金量提高，市场分析的结果表明，如果产品的销售价提高的百分率为，那么月平均销售量减少的百分率为.记改进工艺后，旅游部门销售该纪念品的月平均利润是（元）.
(1)写出与的函数关系式；
(2)改进工艺后，确定该纪念品的售价，使旅游部门销售该纪念品的月平均利润最大.

如图，在平面直角坐标系中，过轴正方向上一点任作一直线，与抛物线相交于两点．一条垂直于轴的直线，分别与线段和直线交于点．
（1）若,求的值；
（2）若为线段的中点，求证：为此抛物线的切线；
（3）试问（2）的逆命题是否成立？说明理由．

已知函数，为实数，（）．
（Ⅰ）若，求函数的极值；
（Ⅱ）若,且函数有三个不同的零点，求实数的取值范围．

设p:实数x满足,其中,
实数满足
（Ⅰ）若且为真，求实数的取值范围；
（Ⅱ）若p是q的必要不充分条件,求实数的取值范围

已知函数（为实数），函数
（1）若，且函数恒成立，求的值；
（2）在（1）条件下，当时, 是单调函数, 求实数k的取值范围；
（3）若, 且为偶函数, 判断的符号（正或负），并说明理由．

某企业利用银行无息贷款，投资400万元引进一条高科技生产流水线，预计每年可获产品利润100万元。但还另需用于此流水线的保养、维修费用第一年10万元，以后每年递增5万元，问至少几年可收回该项投资？（即总利润不小于总支出）

（本小题满分14分）
设函数，函数有唯一的零点，其中实数为常数，，．
（Ⅰ）求的表达式；(Ⅱ)求的值；
(Ⅲ)若且，求证：．

（求100～999中的水仙花数,所谓水仙花数是一个三位数,它的各位数字的立方和等于该数,例如153是一个水仙花数,因为.试编一段程序,找出所有的水仙花数.

（本小题14分）
设是定义在上的单调增函数，满足，
（1）求；      
（2）若，求的取值范围。

（本小题14分）设是定义在上的单调增函数，满足，
（1）求；      （2）若，求的取值范围。

(满分10分)某分公司经销某种品牌产品，每件产品的成本为3元，并且每件产品还需再向总公司交元（）的管理费，预计当每件产品的售价为元（）时，一年的销售量为万件．  
（1）求分公司一年的利润(万元)与每件产品的售价的函数关系式；
（2）当每件产品的售价为多少元时，分公司一年的利润最大，
并求出的最大值

(12分)设函数满足条件f（-1+x）=f（-1-x），且关于x的不等式的解集为
（1）求函数f（x）的解析式；
(2)若时，不等式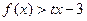恒成立，求实数t的取值范围。

(12分)已知函数f(x)=
（1）判断f(x)的奇偶性，
（2）解不等式f(x)≥