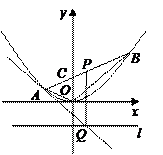如图,在平面直角坐标系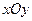 中,过
中,过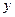 轴正方向上一点
轴正方向上一点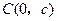 任作一直线,与抛物线
任作一直线,与抛物线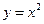 相交于
相交于 两点.一条垂直于
两点.一条垂直于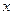 轴的直线,分别与线段
轴的直线,分别与线段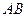 和直线
和直线 交于点
交于点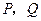 .
.
(1)若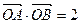 ,求
,求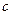 的值;
的值;
(2)若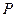 为线段
为线段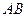 的中点,求证:
的中点,求证: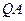 为此抛物线的切线;
为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由.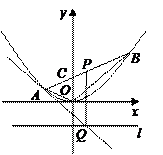
相关知识点
推荐套卷
如图,在平面直角坐标系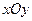 中,过
中,过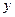 轴正方向上一点
轴正方向上一点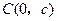 任作一直线,与抛物线
任作一直线,与抛物线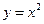 相交于
相交于 两点.一条垂直于
两点.一条垂直于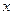 轴的直线,分别与线段
轴的直线,分别与线段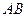 和直线
和直线 交于点
交于点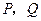 .
.
(1)若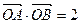 ,求
,求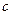 的值;
的值;
(2)若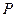 为线段
为线段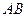 的中点,求证:
的中点,求证: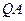 为此抛物线的切线;
为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由.