已知函数f(x)=cosx•sin(x+ )﹣
)﹣ cos2x+
cos2x+ ,x∈R.
,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在闭区间[﹣ ,
, ]上的最大值和最小值.
]上的最大值和最小值.
(本小题满分12分)已知函数
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)设 的三内角分别是A、B、C.若
的三内角分别是A、B、C.若 ,且
,且 ,求
,求 的值.
的值.
(本小题共13分)已知函数 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 在区间
在区间 上的最大值和最小值,及相应的x的值.
上的最大值和最小值,及相应的x的值.
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)在 中,内角
中,内角 所对边的长分别是
所对边的长分别是 ,若
,若 ,求
,求 的面积
的面积 的值.
的值.
设函数 直线
直线
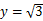 与函数f(x)图像相邻两交点的距离为
与函数f(x)图像相邻两交点的距离为 .
.
(1)求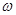 的值;
的值;
(2)若g(x)=af(x)+b在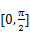 上的最大值为
上的最大值为 ,最小值为1,求a+b的值.
,最小值为1,求a+b的值.
若 (
( ,
, ,已知点
,已知点 ,
, 是函数
是函数 图象上的任意两点,若
图象上的任意两点,若 时,
时, 的最小值为
的最小值为 ,且函数
,且函数 为奇函数.
为奇函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,得到函数
个单位后,得到函数 的图象,求函数
的图象,求函数 的单调递增区间.
的单调递增区间.
(本小题满分14分)已知函数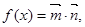 其中向量
其中向量

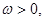 若
若 的图像上相邻两个对称中心的距离大于等于
的图像上相邻两个对称中心的距离大于等于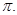
(1)求 的取值范围;
的取值范围;
(2)在 中,
中,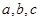 分别是角
分别是角 的对边,
的对边, 当
当 最大时,
最大时, 求
求 的面积最大值.
的面积最大值.
(本小题12分)已知函数 ,
, 。
。
(1)求函数 的最大值和单调递减区间;
的最大值和单调递减区间;
(2)已知 的内角
的内角 的对边分别为
的对边分别为 ,设角
,设角 是
是 的最大角,且
的最大角,且 ,
, .若向量
.若向量 与向量
与向量 垂直,求
垂直,求 的值。
的值。