高中数学多面角及多面角的性质解答题

如图,角终边上一点P的坐标(3,4),将OP绕原点旋转到的位置,试求点的坐标.

（本小题满分13分）已知函数，
（Ⅰ）求函数的最小正周期；
（Ⅱ）记的内角A，B，C的对边长分别为，若，求的值。

求函数在上的最值                

如图，设A是单位圆和轴正半轴的交点，P,Q是单位圆上两点，O是坐标原点，且,.
（1）若点Q的坐标是，求的值；
（2）设函数，求的值域.

（本小题满分12分）
已知平面向量，，函数．
（1）写出函数的单调递减区间；
（2）设，求直线与在闭区间上的图像的所有交点坐标.

（本小题满分12分）已知函数．
（1）求的值；
（2）求函数的最小正周期和单调增区间；
（3）说明的图像是如何由函数的图像变换所得．

设函数
（Ⅰ）当，求函数的单调区间与极值；
（Ⅱ）若函数在上是增函数，求实数的取值范围．

已知向量，且函数在时取得最小值．
（Ⅰ）求的值；
（Ⅱ）在中，分别是内角的对边，若，，，求的值．

已知函数（）的周期为.
（1）当时，求函数的值域；
（2）已知的内角，，对应的边分别为，，，若，且，，求的面积.

已知函数（），其中，，满足以下两个条件：①两条相邻对称轴之间的距离为；②．
（Ⅰ）求函数的解析式；
（Ⅱ）求函数在内的单调递增区间；
（Ⅲ）若方程在内有个不等实根，求实数的取值范围．

（本题12分）已知,,．
（1）求的单调递减区间;
（2）若函数，求当时,的最大值．

（本小题满分12分）
已知函数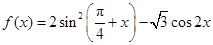
（1）求函数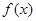的最大值，以及取到最大值时所对应的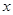的集合；
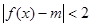（2）在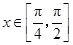上恒成立，求实数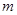的取值范围。

（本小题满分12分）已知，．
（1）若，求的值；
（2）若，求的单调递增区间．

设．
（1）求的最大值及最小值周期；
（2）在中，角的对边分别为，锐角满足，求的值

.定义域为R的函数f(x)=a-2bcosx(b>0)的最大值为,最小值为,求a,b 的值.