已知函数 (
(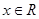 ),其中
),其中 ,
, ,
,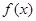 满足以下两个条件:①两条相邻对称轴之间的距离为
满足以下两个条件:①两条相邻对称轴之间的距离为 ;②
;②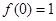 .
.
(Ⅰ)求函数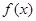 的解析式;
的解析式;
(Ⅱ)求函数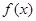 在
在 内的单调递增区间;
内的单调递增区间;
(Ⅲ)若方程 在
在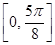 内有
内有 个不等实根,求实数
个不等实根,求实数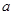 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知函数 (
(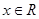 ),其中
),其中 ,
, ,
,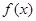 满足以下两个条件:①两条相邻对称轴之间的距离为
满足以下两个条件:①两条相邻对称轴之间的距离为 ;②
;②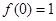 .
.
(Ⅰ)求函数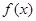 的解析式;
的解析式;
(Ⅱ)求函数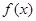 在
在 内的单调递增区间;
内的单调递增区间;
(Ⅲ)若方程 在
在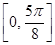 内有
内有 个不等实根,求实数
个不等实根,求实数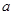 的取值范围.
的取值范围.