高中数学几何不等式试题

已知a≥b>0，求证：2a³－b³≥2ab²－a²b.

“关于的不等式对于一切实数都成立”是“”的

A．充要条件	B．充分非必要条件
C．必要非充分条件	D．既非充分又非必要条件

不等式表示的区域在直线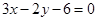的(  )

A．右上方

B．右下方

C．左上方

D．左下方

设f(x)是定义在R上的奇函数，且f(－1)＝0，当x＞0时，(x²＋1)f′(x)－2xf(x)＜0，则不等式f(x)＞0的解集为________．

已知实数x，y满足条件，则z=x+3y的最小值是（   ）

A．

B．

C．12

D．－12

设，求的值.

仔细阅读下面问题的解法：
设A＝[0，1]，若不等式2^1－x+a>0在A上有解，求实数a的取值范围.
解：令f(x)＝2^1－x+a，因为f(x)>0在A上有解。

＝2+a>0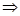a>-2
学习以上问题的解法，解决下面的问题，已知：函数f(x)=x²+2x+3(-2≤x≤-1).
①求f(x)的反函数f^-1(x)及反函数的定义域A；
②设B＝，若A∩B≠,求实数a的取值范围.

函数是定义域为的可导函数，且对任意实数都有成立．若当时，不等式成立，设，，，则，，的大小关系是（   ）

A．

B．

C．

D．

在如图所示的锐角三角形空地中, 欲建一个面积不小于300m²的内接矩形花园(阴影部分), 则其边长 $x$(单位 $m$)的取值范围是 （   ）

A．

[15,20]

B．

[12,25]

C．

[10,30]

D．

[20,30]

已知函数的图象经过点，则不等式的解为_________;

已知正数a、b、c满足，求证：

已知，且，则的值（   ）

A．大于零

B．小于零

C．不大于零

D．不小于零

若a、b、c、d均为实数，使不等式都成立的一组值（a、b、c、d）是         。（只要写出适合条件的一组值即可）

解关于的不等式:＜.

已知,.若同时满足条件:
①或;② ,. 则的取值范围是________.