吉林省吉林市普通高中高二上学期期末理数学试卷
命题“对任意的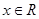 ,都有
,都有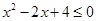 ”的否定为
”的否定为
A.存在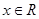 ,使 ,使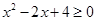 |
B.对任意的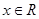 ,都有 ,都有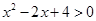 |
C.存在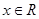 ,使 ,使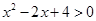 |
D.存在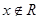 ,使 ,使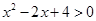 |
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
以下四组向量:① ,
, ;②
;② ,
, ;③
;③ ,
, ;④
;④ ,
,
其中互相平行的是.
| A.②③ | B.①④ | C.①②④ | D.①②③④ |
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
对抛物线 ,下列描述正确的是
,下列描述正确的是
A.开口向上,焦点为 |
B.开口向上,焦点为 |
C.开口向右,焦点为 |
D.开口向右,焦点为 |
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
“关于 的不等式
的不等式 对于一切实数
对于一切实数 都成立”是“
都成立”是“ ”的
”的
| A.充要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.既非充分又非必要条件 |
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
在 中,
中, ,给出
,给出 满足的条件,就能得到动点
满足的条件,就能得到动点 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
| 条件 |
方程 |
① 周长为10 周长为10 |
 |
② 面积为10 面积为10 |
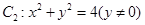 |
③ 中, 中, |
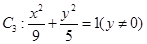 |
则满足条件①、②、③的点 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A.  、
、 、
、 B.
B.  、
、 、
、
C.  、
、 、
、 D.
D.  、
、 、
、
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
已知直线 与双曲线
与双曲线 ,有如下信息:联立方程组:
,有如下信息:联立方程组: , 消去
, 消去 后得到方程
后得到方程 ,分类讨论:(1)当
,分类讨论:(1)当 时,该方程恒有一解;(2)当
时,该方程恒有一解;(2)当 时,
时, 恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是
恒成立。在满足所提供信息的前提下,双曲线离心率的取值范围是
A. |
B. |
C. |
D. |
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
已知F1,F2是椭圆 的两焦点,过点F2的直线交椭圆于A,B两点.在
的两焦点,过点F2的直线交椭圆于A,B两点.在
△AF1B中,若有两边之和是10,则第三边的长度为
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
已知数列 的前n项和
的前n项和
(1)求数列 的通项公式,并证明
的通项公式,并证明 是等差数列;
是等差数列;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
命题 :方程
:方程 表示的曲线是焦点在y轴上的双曲线,命题
表示的曲线是焦点在y轴上的双曲线,命题 :方程
:方程 无实根,若
无实根,若 ∨
∨ 为真,
为真, 为真,求实数
为真,求实数 的取值范围.
的取值范围.
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
已知定点 和定直线
和定直线 ,动点与定点
,动点与定点 的距离等于点
的距离等于点 到定直线
到定直线 的距离,记动点
的距离,记动点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程.
的方程.
(2)若以 为圆心的圆与曲线
为圆心的圆与曲线 交于
交于 、
、 不同两点,且线段
不同两点,且线段 是此圆的直径时,求直线
是此圆的直径时,求直线 的方程.
的方程.
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
如图,直三棱柱(侧棱垂直于底面的棱柱) ,底面
,底面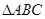 中
中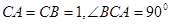 ,棱
,棱 ,
, 分别为
分别为 的中点.
的中点.
(1)求 >的值;
>的值;
(2)求证:
来源:2013-2014学年吉林省吉林市普通高中高二上学期期末理数学试卷
 的焦距为
的焦距为



 中,
中, ,则
,则 等于
等于 是等比数列,前
是等比数列,前 项和为
项和为 ,
, ,则
,则




 为抛物线
为抛物线 上的动弦,且
上的动弦,且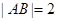 , 则弦
, 则弦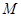 到
到 轴的最小距离为
轴的最小距离为

 ,且
,且 ,则下列不等式中,恒成立的是
,则下列不等式中,恒成立的是



 是椭圆
是椭圆 上的一点,
上的一点,  是焦点, 且
是焦点, 且 ,则△
,则△ 的面积是
的面积是



 满足条件
满足条件 ,则
,则 的最大值为
的最大值为  ,虚轴长为4, 则该双曲线的标准方程是
,虚轴长为4, 则该双曲线的标准方程是  ,若数列
,若数列 满足
满足 ,则
,则
 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, 的大小;
的大小; ,求
,求 和
和 的值.
的值. 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点. 是第一象限内该椭圆上的一点,
是第一象限内该椭圆上的一点, ,求点
,求点 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且
,且 为锐角(其
为锐角(其 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号