[福建]2013届福建省漳州市七校高三第三次联考理科数学试卷
若a R,则a>2是(a-1)(a-2)>0的
R,则a>2是(a-1)(a-2)>0的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 C.既不充分又不必要条件
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于
A. |
B. |
C. |
D. |
曲线C:y= ,则x轴与C及直线x=1、x=2围成的封闭图形的面积为
,则x轴与C及直线x=1、x=2围成的封闭图形的面积为
| A.1n2一1 | B.1一1n2 | C.1n2 | D.2-1n2 |
已知抛物线y2 =4x的焦点为F,准线为 交于A,B两点,若△FAB为直角三角形,则双曲线的离心率是
交于A,B两点,若△FAB为直角三角形,则双曲线的离心率是
A. |
B. |
C.2 | D. |
我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径. “开立圆术”相当于给出了已知球的体积 ,求其直径
,求其直径 的一个近似公式
的一个近似公式 . 人们还用过一些类似的近似公式. 根据
. 人们还用过一些类似的近似公式. 根据 判断,下列近似公式中最精确的一个是( )
判断,下列近似公式中最精确的一个是( )
A. |
B. |
C. |
D. |
从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数,其中奇数的个数为______。
如图所示是三棱锥D—ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DO与AB所成角的余弦值等于______。
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有 名获得优秀,求
名获得优秀,求 的分布列和数学期望。
的分布列和数学期望。
如图所示,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,点
,点 在线段
在线段 上,
上, 平面
平面 .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)若 ,
, ,求二面角
,求二面角 的正切值.
的正切值.
已知函数 ·
· (其中
(其中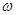 >o),且函数
>o),且函数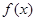 的最小正周期为
的最小正周期为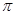
(I)求f(x)的最大值及相应x的取值
(Ⅱ)将函数y= f(x)的图象向左平移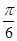 单位长度,再将所得图象各点的横坐标缩小为原来的
单位长度,再将所得图象各点的横坐标缩小为原来的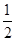 倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
倍(纵坐标不变)得到函数y=g(x)的图象.求函数g(x)的单调区间.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 与椭圆
与椭圆 相切
相切 ,直线
,直线 与
与 轴交于点
轴交于点 ,当
,当 为何值时
为何值时 的面积有最小值?并求出最小值.
的面积有最小值?并求出最小值.
已知函数 (
( 为常数,
为常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与 轴平行.
轴平行.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,其中
,其中 为
为 的导函数.证明:对任意
的导函数.证明:对任意 .
.
已知圆 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为 (
( 为参数).若直线
为参数).若直线 与圆
与圆 相交于
相交于 ,
, 两点,且
两点,且 .
.
(Ⅰ)求圆 的直角坐标方程,并求出圆心坐标和半径;
的直角坐标方程,并求出圆心坐标和半径;
(Ⅱ)求实数 的值.
的值.
 = ( )
= ( ) ,则函数
,则函数 的最小正周期是
的最小正周期是



 ,b
,b ,且a⊥b.若
,且a⊥b.若 满足不等式
满足不等式 ,则
,则 的取值范围为
的取值范围为



 为奇函数,且
为奇函数,且 ,则当
,则当 =( )
=( )




 的首项为2,数列
的首项为2,数列 为等差数列且
为等差数列且 (
( ).若
).若 ,
, ,则
,则 .
. ,
, .若同时满足条件:
.若同时满足条件: 或
或 ;②
;② ,
, . 则
. 则 的取值范围是________.
的取值范围是________.
 的逆矩阵
的逆矩阵 ;
;  经过矩阵
经过矩阵 ,求直线
,求直线 ,
,
 ,解关于
,解关于 的不等式
的不等式 ;
;  的图象恒在函数
的图象恒在函数 图象的上方,求实数
图象的上方,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号