某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为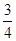 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有 名获得优秀,求
名获得优秀,求 的分布列和数学期望。
的分布列和数学期望。
推荐套卷
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为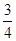 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有 名获得优秀,求
名获得优秀,求 的分布列和数学期望。
的分布列和数学期望。