(本小题满分13分)
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”。如图所示的路径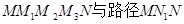 都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点
都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点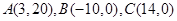 处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。
处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。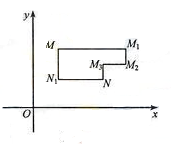
(I)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(II)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度值和最小。
已知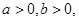 且
且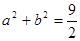 ,若
,若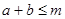 恒成立,
恒成立,
(1)求 的最小值;(2)若
的最小值;(2)若 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
不等式(-1)na<2+ 对任意n∈N*恒成立,求实数a的取值范围.
对任意n∈N*恒成立,求实数a的取值范围.
如图,动物园要围成相同面积的长方形虎笼四间.一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围成36m长的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
(2)若使每间虎笼的面积为24m2,则每间虎笼的长、宽各设计为多少时,可使围成的四间虎笼的钢筋网总长最小?
函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围;
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),总成本为G(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:R(x)= 假定该产品产销平衡,那么根据上述统计规律求下列问题.
假定该产品产销平衡,那么根据上述统计规律求下列问题.
(1)要使工厂有赢利,产量x应控制在什么范围内?
(2)工厂生产多少台产品时,可使赢利最多?
已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a、b的值.