已知△ABC的一个内角为120°,并且三边长构成公差为4的等差数列,则△ABC的面积为 .
在△ABC中,角A,B,C对应的边分别是a,b,c,已知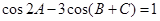 .
.
(1)求角A的大小;
(2)若△ABC的面积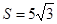 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
已知函数 ,其中
,其中 ,
, .若函数
.若函数 相邻两对称轴的距离等于
相邻两对称轴的距离等于 .
.
(1)求 的值;并求函数
的值;并求函数 在区间
在区间 的值域;
的值域;
(2)在△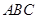 中,
中, 、
、 、
、 分别是角
分别是角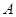 、
、 、
、 的对边,若
的对边,若
 ,求边
,求边 、
、 的长.
的长.
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3 ,b﹣c=2,cosA=﹣
,b﹣c=2,cosA=﹣ .
.
(Ⅰ)求a和sinC的值;
(Ⅱ)求cos(2A+ )的值.
)的值.
在△ABC中,角A,B,C的对边分别为a,b,c,向量 =(cosC,sin
=(cosC,sin ),向量
),向量 =(sin
=(sin ,cosC),且
,cosC),且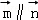 .
.
(1)求角C的大小;
(2)若a2=2b2+c2,求tanA的值.
在△ABC中,a,b,c分别为∠A,∠B,∠C的对边,且c>b>a,若向量 =(a-b,1)和
=(a-b,1)和 =(b-c,1)平行,且sin B=
=(b-c,1)平行,且sin B= ,当△ABC的面积为
,当△ABC的面积为 时,则b=()
时,则b=()
A. |
B.2 | C.4 | D.2+ |
(本小题满分12分)设 的内角
的内角 所对应的边长分别是
所对应的边长分别是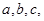 且
且
(Ⅰ)当 时,求
时,求 的值;
的值;
(Ⅱ)当 的面积为3时,求
的面积为3时,求 的值.
的值.
(本小题满分16分)如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是 ,点
,点 在直径
在直径 上,且
上,且 .
.
(1)若 ,求
,求 的长;
的长;
(2)设 , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
设
的内角
的对边分别为
,且
为钝角.
(1)证明:
;
(2)求
的取值范围.
如图,塔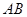 底部为点
底部为点 ,若
,若 两点相距为100m并且与点
两点相距为100m并且与点 在同一水平线上,现从
在同一水平线上,现从 两点测得塔顶
两点测得塔顶 的仰角分别为
的仰角分别为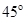 和
和 ,则塔
,则塔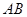 的高约为(精确到0.1m,
的高约为(精确到0.1m, ,
, )()
)()
| A.36.5 | B.115.6 | C.120.5 | D.136.5 |