若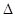 ABC三个内角A、B、C的对边分别为a,b,c,且a=1,
ABC三个内角A、B、C的对边分别为a,b,c,且a=1, B=45o,S
B=45o,S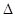 ABC=2,则sinA=( ).
ABC=2,则sinA=( ).
(A)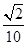 (B)
(B)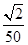 (C)
(C) (D)
(D)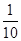
已知函数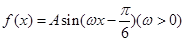 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是 ,且满足,
,且满足,
(1)求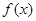 的单调递减区间;
的单调递减区间;
(2)在钝角△ABC中,a、b、c分别为角A、B、C的对边,sinB=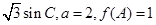 ,求△ABC的面积。
,求△ABC的面积。
如图所示,某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料,已知已有两面墙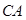 、
、 的夹角为
的夹角为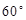 (即
(即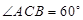 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 米),为了使得仓库的面积尽可能大,记
米),为了使得仓库的面积尽可能大,记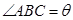 ,问当
,问当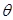 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 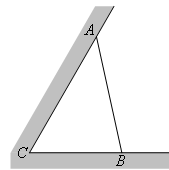
 中,角
中,角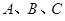 所对的边分别为
所对的边分别为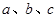 ,下列命题正确的是________(写出正确命题的编号).
,下列命题正确的是________(写出正确命题的编号).
①若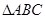 最小内角为
最小内角为 ,则
,则 ;
;
②若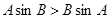 ,则
,则 ;
;
③存在某钝角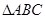 ,有
,有 ;
;
④若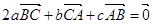 ,则
,则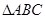 的最小角小于
的最小角小于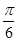 ;
;
⑤若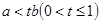 ,则
,则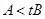 .
.
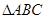 中,角
中,角 所对的边分别为
所对的边分别为 ,下列命题正确的是________(写出正确命题的编号).
,下列命题正确的是________(写出正确命题的编号).
①若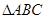 最小内角为
最小内角为 ,则
,则 ;
;
②若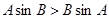 ,则
,则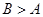 ;
;
③存在某钝角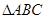 ,有
,有 ;
;
④若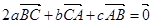 ,则
,则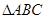 的最小角小于
的最小角小于 ;
;
⑤若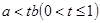 ,则
,则 .
.
已知向量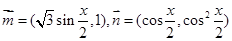 .记
.记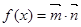
(I)求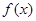 的最小正周期及单调增区间;
的最小正周期及单调增区间;
(Ⅱ)在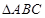 中,角
中,角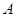 ,
,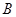 ,
,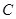 的对边分别为
的对边分别为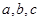 若
若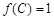 ,
,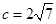 ,
,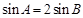 ,求
,求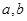 的值.
的值.
已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若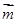 =(-cos
=(-cos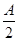 ,sin
,sin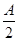 ),
),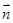 =(cos
=(cos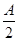 ,sin
,sin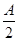 ),a=2
),a=2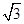 ,且
,且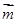 ·
·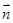 =
=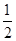 .
.
(1)若△ABC的面积S=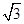 ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范围.
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.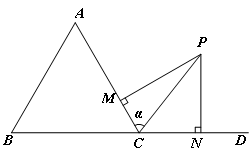
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 、
、 、
、 ,已知向量
,已知向量 、
、 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求
,求 面积的最大值.
面积的最大值.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
.
(1) 求角 的大小;
的大小;
(2) 当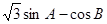 取得最大值时,请判断
取得最大值时,请判断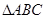 的形状.
的形状.
已知向量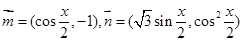 ,设函数
,设函数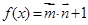
(1)求函数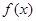 的单调递增区间;
的单调递增区间;
(2)在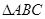 中,角
中,角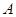 、
、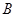 、
、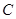 的对边分别为
的对边分别为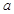 、
、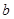 、
、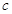 ,且满足
,且满足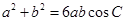 ,
,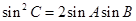 ,求
,求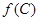 的值.
的值.