高中数学函数迭代填空题

已知数列{a_n}（n∈N_＋）是各项均为正数且公比不等于1的等比数列，对于函数y＝f（x），若数列{lnf（a_n）}为等差数列，则称函数f（x）为“保比差数列函数”.现有定义在（0，＋∞）上的四个函数：①f（x）＝e^x；②f（x）＝；③f（x）＝kx（k＞0）；④f（x）＝ax²＋b（a＞0且b＞0）.则为“保比差数列函数”的是_______________.

若函数f（x）为定义域D上的单调函数,且存在区间（其中a<b）,使得当x∈[a,b]时,f（x）的取值范围恰为[a,b],则称函数f（x）是D上的“正函数”,若是上的正函数，则实数k的取值范围是           

对于函数，若存在区间=[]()，使得，则称区间为函数的一个“稳定区间”.给出下列四个函数：
① ② ③  ④
其中存在“稳定区间”的函数有_____________（填正确序号）.

已知函数及其导数，若存在，使得，则称是的一个“巧值点”，下列函数中，有“巧值点”的是         （填上正确的序号）
（1）；
（2）；
（3）；
（4）；
（5）

定义域为的函数的图像的两个端点为，是图像上任意一点，其中，向量,若不等式恒成立，则称函数在上“阶线性近似”，若函数在上“阶线性近似”，则实数的取值范围是                    

设与是定义在同一区间上的两个函数，若函数在上有两个不同的零点，则称和在上是“关联函数”，区间称为“关联区间”．若与在[0,3]上是“关联函数”，则的取值范围是          ．

设函数的定义域为，若，使得成立，则称函数为“美丽函数”.下列所给出的五个函数：
①；②；③；④；⑤．
其中是“美丽函数”的序号有          ．

在实数的原有运算法则中，我们补充定义新运算“”如下：当时，；当时，。则函数，则的值域为：___________。

设定义域为的函数同时满足以下三个条件时，称为“友谊函数”：
（1）对任意的；
（2）；
（3）若，则有成立，
则下列判断正确的有_________
①为“友谊函数”，则；
②函数在区间上是“友谊函数”；
③若为“友谊函数”，且.

如果对于函数的定义域内任意两个自变量的值，当时，都有且存在两个不相等的自变量，使得，则称为定义域上的不严格的增函数．已知函数的定义域、值域分别为，，，且为定义域上的不严格的增函数，那么这样的函数共有________个．

已知点是函数的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论成立.运用类比思想方法可知，若点图象上的不同两点，则类似地有________________成立.

函数，其中，若动直线与函数的图像有三个不同的交点，它们的横坐标分别为，则是否存在最大值？若存在，在横线处填写其最大值；若不存在，直接填写“不存在”______________．

对于大于1的自然数m的三次幂，可用奇数进行以下方式的“分裂”：2³＝，3³＝，4³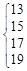＝， ，仿此，若m³的“分裂数”中有一个是2015，则m＝___________.

对于大于1的自然数m的三次幂，可用奇数进行以下方式的“分裂”：2³＝，3³＝，4³＝， ，仿此，若m³的“分裂数”中有一个是2015，则m＝___________.

符号表示不超过的最大整数，如［］＝３，＝－２，定义函数：，则下列命题正确的序号是            ．
① ;
② 方程＝有无数个解； 
③ 函数是增函数；
④ 函数是奇函数.
⑤ 函数的定义域为Ｒ，值域为［０，１］.