(本小题共8分)
已知函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y),且当x>0时,f(x)>0,f(-1)=-2,求f(x)在[-2,1]上的值域。
(本小题满分12分)
已知函数
(1)若函数 在
在 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围;
(2)当 时,求
时,求 在
在 上的最大值和最小值;
上的最大值和最小值;
(3) 当 时,求证:对大于1的任意正整数
时,求证:对大于1的任意正整数 ,都有
,都有 。
。
(本小题满分14分)
已知函数 .
.
(Ⅰ)函数 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;
(Ⅲ)试证明: (
( )。
)。
(本小题满分14分)
已知函数f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)讨论f(x)的单调性;
(2)设g(x)=(a2+ )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
若存在实数x∈[2,4],使x2-2x+5-m<0成立,则m的取值范围为
| A.(13,+∞) | B.(5,+∞) | C.(4,+∞) | D.(-∞,13) |
已知定义域为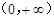 的函数
的函数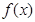 满足:①对任意
满足:①对任意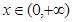 ,恒有
,恒有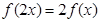 成立;当
成立;当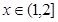 时,
时,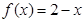 。给出如下结论:
。给出如下结论:
①对任意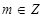 ,有
,有 ;②函数
;②函数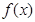 的值域为
的值域为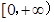 ;③存在
;③存在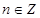 ,使得
,使得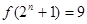 ;④“函数
;④“函数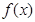 在区间
在区间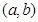 上单调递减”的充要条件是 “存在
上单调递减”的充要条件是 “存在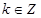 ,使得
,使得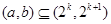 ”。其中所有正确结论的序号是 。
”。其中所有正确结论的序号是 。
已知函数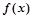 定义在R上的奇函数,当
定义在R上的奇函数,当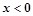 时,
时,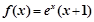 ,给出下列命题:
,给出下列命题:
①当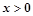 时,
时,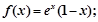 ②函数
②函数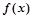 有2个零点
有2个零点
③ 的解集为
的解集为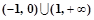 ④
④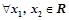 ,都有
,都有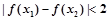
其中正确命题个数是:
| A.1 | B.2 | C.3 | D.4 |
函数 在
在 处有极值10,则m,n的值是( )
处有极值10,则m,n的值是( )
A. |
B. |
C. |
D. |
定义在 上的函数
上的函数 ,
, ,当
,当 时,
时, .且对任意的
.且对任意的 有
有 。
。
(1)证明: ;
;
(2)证明:对任意的 ,恒有
,恒有 ;
;
(3)证明: 是
是 上的增函数;
上的增函数;
(4)若 ,求
,求 的取值范围。
的取值范围。