[江西]2013届江西省南昌市高三上学期调研考试理科数学试卷
集合A={x||x|≤4,x∈R},B={x|(x+5)(x-a)≤0},则“AÍB”是“a>4”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中,m,n表示两条不同的直线,a,b,γ表示三个不同的平面
①若m⊥a,n∥a,则m⊥n;
②若a⊥γ,b⊥γ,则a∥b;
③若m∥a,n∥a,则m∥n;
④若a∥b,b∥γ,m⊥a,则m⊥γ.
正确的命题是
| A.①③ | B.②③ | C.①④ | D.②④ |
已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
A.-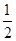 |
B.1 | C.-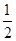 或1 或1 |
D.-1或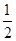 |
下图是某次考试对一道题评分的算法框图,其中x1,x2,x3为三个评卷人对该题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=8.5时,x3等于
| A.11 | B.10 | C.8 | D.7 |
右图是函数y=sin(ωx+j)(x∈R)在区间[-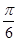 ,
,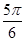 ]上的图像,
]上的图像,
为了得到这个函数的图像,只要将y=sinx(x∈R)的图像上所有点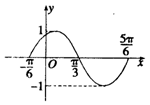
A.向左平移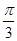 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的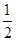 倍, 倍,纵坐标不变。 |
B.向左平移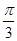 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 |
C.向左平移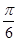 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的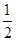 倍,纵坐标不变。 倍,纵坐标不变。 |
D.向左平移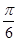 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 |
若存在实数x∈[2,4],使x2-2x+5-m<0成立,则m的取值范围为
| A.(13,+∞) | B.(5,+∞) | C.(4,+∞) | D.(-∞,13) |
已知奇函数f(x)在[-1,0]上为单调递减函数,又a,b为锐角三角形两内角,下列结论正确的是
| A.f(cosa)> f(cosb) | B.f(sina)> f(sinb) |
| C.f(sina)> f(cosb) | D.f(sina)<f(cosb) |
△ABC所在平面上一点P满足 +
+ +
+ =
= ,则△PAB的面积与△ABC的面积之比为
,则△PAB的面积与△ABC的面积之比为
| A.2∶3 | B.1∶3 | C.1∶4 | D.1∶6 |
如图所示的四个容器高度都相同,将水从容器顶部一个小孔以相同的速度注入其中,注满为止.用下面对应的图像显示该容器中水面的高度h和时间t之间的关系,其中不正确的是
| A.1个 | B.2个 | C.3个 | D.4个 |
已知整数对的序列如下:(1,1),(1,2),(2,1),(1,3),
(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),
(2,4)…,则第57个数对是
(本小题满分12分)已知向量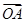 =3i-4j,
=3i-4j,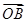 =6i-3j,
=6i-3j,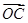 =(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
=(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
(1)A,B,C能够成三角形,求实数m应满足的条件。
(2)对任意m∈[1,2]使不等式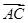 2≤-x2+x+3恒成立,求x的取值范围
2≤-x2+x+3恒成立,求x的取值范围
列车提速可以提高铁路运输量.列车运行时,前后两车必须要保持一个“安全间隔距离d(千米)”,“安全间隔距离d(千米)”与列车的速度v(千米/小时)的平方成正比(比例系数k=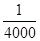 ).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=
).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=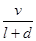 最大?
最大?
(本小题满分12分)
如图,边长为a的正方体ABCD-A1B1C1D1中,E为CC1的中点.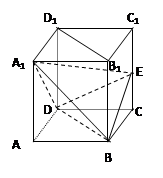
(1)求直线A1E与平面BDD1B1所成的角的正弦值
(2)求点E到平面A1DB的距离
(本小题满分13分)
在数列{an}中,a1=1,an=n2[1+ +
+ +…+
+…+ ] (n≥2,n∈N)
] (n≥2,n∈N)
(1)当n≥2时,求证: =
=
(2)求证:(1+ )(1+
)(1+ )…(1+
)…(1+ )<4
)<4
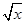 ,直线y=x-2及y轴所围成的图形的面积为
,直线y=x-2及y轴所围成的图形的面积为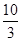
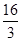
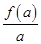 ,
, 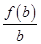 ,
,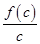 的大小关系是
的大小关系是 
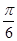 )=
)=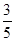 。求cosa
。求cosa )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号