(本小题满分14分)
已知函数f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)讨论f(x)的单调性;
(2)设g(x)=(a2+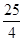 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
相关知识点
推荐套卷
(本小题满分14分)
已知函数f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)讨论f(x)的单调性;
(2)设g(x)=(a2+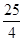 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.