[北京]2012-2013学年北京市东城区(南片)高一上学期期末考试数学试卷
设P={x|x<4},Q={x|-2<x<2},则
A.P Q Q |
B.Q P P |
C.P 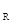 Q Q |
D.Q 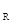 P P |
下列函数在区间[0,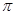 ]上是减函数的是
]上是减函数的是
| A.y="sin" x | B.y="cos" x | C.y="tan" x | D.y=2 |
已知a=lg3+lg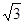 ,b=
,b=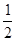 lg9,c=lg2,则a,b,c的大小关系是
lg9,c=lg2,则a,b,c的大小关系是
| A.b<a<c | B.c<a<b | C.a<b<c | D.c<b<a |
要得到函数y=cos(2x+1)的图象,只需将函数y=cos2x的图象
| A.向左平移1个单位 | B.向右平移1个单位 |
C.向左平移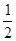 个单位 个单位 |
D.向右平移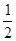 个单位 个单位 |
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(1)=
| A.-3 | B.-1 | C.1 | D.3 |
函数f(x)=xcosx在区间[0,2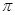 ]上的零点个数为
]上的零点个数为
| A.2 | B.3 | C.4 | D.5 |
如图所示,单位圆中弧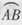 的长为x,f(x)表示孤
的长为x,f(x)表示孤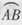 与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是
与弦AB所围成的弓形面积的2倍,则函数y=f(x)的图象是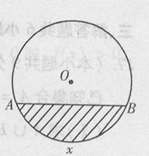
定义在R上的函数f(x)满足f(x)-f(-x)=0,且对任意x,x∈[0,+ )(x
)(x x),都有
x),都有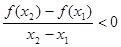 ,则
,则
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
函数y=f(x)的图象如图所示,则不等式f(x)<f(-x)+x的解集为______。
(本小题共9分)
已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R
(Ⅰ)求A∪B,(C  A)∩B;
A)∩B;
(Ⅱ)若A∩C≠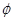 ,求a的取值范围。
,求a的取值范围。
(本小题共9分)
已知函数f(x)=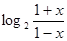 。
。
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并证明;
(Ⅲ)判断函数f(x)在定义域上的单调性,并用定义证明。
(本小题共9分)
已知函数f(x)=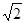 sin(2x+
sin(2x+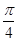 ),x∈R.
),x∈R.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[-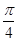 ,
,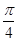 ]上的最大值和最小值。
]上的最大值和最小值。
(本小题共9分)
已知函数f(x)=Asin(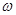 x+
x+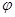 )(x∈R,
)(x∈R,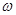 >0,0<
>0,0<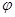 <
<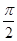 )的部分图象如图所示。
)的部分图象如图所示。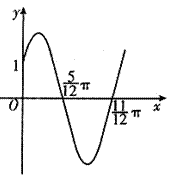
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数g(x)=f(x-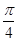 )的单调递增区间。
)的单调递增区间。
(本小题共8分)
已知函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y),且当x>0时,f(x)>0,f(-1)=-2,求f(x)在[-2,1]上的值域。
(本小题共8分)
提高二环路的车辆通行能力可有效改善整个城区的交通状况,在一般情况下,二环路上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数。当二环路上的车流密度达到600辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过60辆/千米时,车流速度为80千米/小时,研究表明:当60≤x≤600时,车流速度v是车流密度x的一次函数。
(Ⅰ)当0≤x≤600时,求函数f(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过二环路上某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值。(精确到1辆/小时)
 为第二象限角,sin
为第二象限角,sin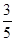 ,则cos
,则cos
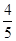
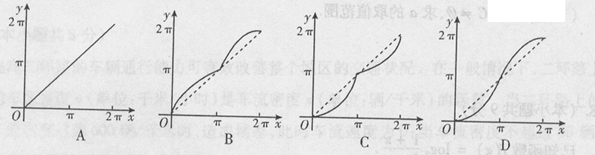
 1)的图象可能是
1)的图象可能是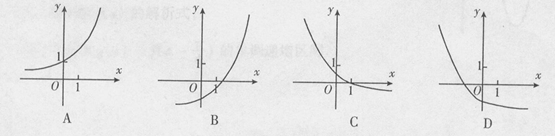
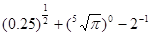 =_______。
=_______。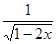 的定义域是________。
的定义域是________。 ,x∈R,且
,x∈R,且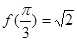 ,则A=________。
,则A=________。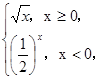 则f(f(-4))=______。
则f(f(-4))=______。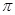 +
+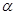 )=2,则
)=2,则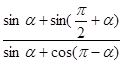 =______。
=______。 粤公网安备 44130202000953号
粤公网安备 44130202000953号