高中数学函数迭代试题

已知函数是定义在上的奇函数，当 时，，且。
（1）求的值，（2）求的值.

在为奇函数，，当时，，则        。

已知函数对任意都有，若的象关于直线对称，且，则(   )

A．2

B．3

C．4

D．0

已知定义在实数集上的函数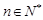，，其导函数记为，
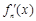（1）设函数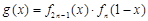,求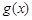的极大值与极小值；
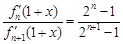(2）试求关于的方程在区间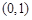上的实数根的个数。

函数
（Ⅰ）判断并证明函数的奇偶性；
（Ⅱ）若，证明函数在上单调递增；
（Ⅲ）在满足（Ⅱ）的条件下，解不等式.

偶函数满足，当时, ，则关于的方程在上解的个数是（ ）

A．1

B．2

C．3

D．4

已知指数函数满足：g(2)=4，定义域为的函数
是奇函数。
（1）确定的解析式；（2）求m，n的值；
（3）若对任意的，不等式恒成立，求实数的取值范围

设f(x)是周期为2的奇函数，当0≤x≤1时，f(x)＝2x(1－x)，则f(－)＝       (　 　)
A．－     B．－        C  .  D.

设函数是定义在上的以为周期的偶函数，若，则实数的取值范围是(     )

A．

B．

C．

D．

已知函数．
（Ⅰ）若为定义域上的单调增函数，求实数的取值范围；
（Ⅱ）当时，求函数的最大值；
（Ⅲ）当时，且，证明：.

f (x)是定义在(0,+∞)上的非负可导函数 ，且满足，若， ，则的大小关系是（   ）

A．

B．

C．

D．

已知函数，
（1）若函数在处的切线方程为，求实数的值；
（2）若在其定义域内单调递增，求的取值范围.

设是定义在上的函数，当，且时，有．
（1）证明是奇函数；
（2）当时，（a为实数）. 则当时，求的解析式；
（3）在（2）的条件下，当时，试判断在上的单调性，并证明你的结论.

设
（1）求，并求数列的通项公式.   
（2）已知函数在上为减函数，设数列的前的和为，
求证：

已知函数在 处的切线方程为.
(1)求函数的解析式；
(2)若关于的方程恰有两个不同的实根，求实数的值 ；
(3)数列满足，，求的整数部分.