设 是定义在
是定义在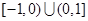 上的函数,当
上的函数,当 ,且
,且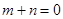 时,有
时,有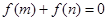 .
.
(1)证明 是奇函数;
是奇函数;
(2)当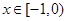 时,
时, (a为实数). 则当
(a为实数). 则当 时,求
时,求 的解析式;
的解析式;
(3)在(2)的条件下,当 时,试判断
时,试判断 在
在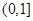 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
相关知识点
推荐套卷
设 是定义在
是定义在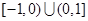 上的函数,当
上的函数,当 ,且
,且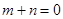 时,有
时,有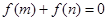 .
.
(1)证明 是奇函数;
是奇函数;
(2)当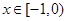 时,
时, (a为实数). 则当
(a为实数). 则当 时,求
时,求 的解析式;
的解析式;
(3)在(2)的条件下,当 时,试判断
时,试判断 在
在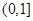 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.