已知数列 满足
满足 ,
, ,(
,( )
)
(1)若 ,数列
,数列 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(2)若 ,试写出
,试写出 对任意
对任意 成立的充要条件,并证明你的结论.
成立的充要条件,并证明你的结论.
已知数列 的前
的前 项和为
项和为 满足
满足 .
.
(1)函数 与函数
与函数 互为反函数,令
互为反函数,令 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(2)已知数列 满足
满足 ,证明:对任意的整数
,证明:对任意的整数 ,有
,有 .
.
已知数列 的通项公式为
的通项公式为 ,数列
,数列 的通项公式为
的通项公式为 ,
,
设 若在数列
若在数列 中,
中, 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
.将正奇数按下表的规律填在5列的数表中,则第20行第3列的数字与第20行第2列数字的和为________.
| |
1 |
3 |
5 |
7 |
| 15 |
13 |
11 |
9 |
|
| |
17 |
19 |
21 |
23 |
| 31 |
29 |
27 |
25 |
|
| |
|
|
|
|
在数列 中,
中, .从数列
.从数列 中选出
中选出 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为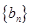 ,并称
,并称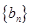 为数列
为数列 的
的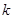 项子列.例如数列
项子列.例如数列 、
、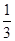 、
、 、
、 为
为 的一个
的一个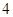 项子列.
项子列.
(1)试写出数列 的一个
的一个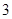 项子列,并使其为等比数列;
项子列,并使其为等比数列;
(2)如果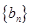 为数列
为数列 的一个
的一个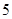 项子列,且
项子列,且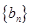 为等差数列,证明:
为等差数列,证明: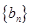 的公差
的公差 满足
满足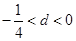 ;
;
(3)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等比数列,证明:
为等比数列,证明: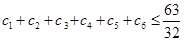 .
.
在数列 中,
中, .从数列
.从数列 中选出
中选出 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为 ,并称
,并称 为数列
为数列 的
的 项子列.例如数列
项子列.例如数列 、
、 、
、 、
、 为
为 的一个
的一个 项子列.
项子列.
(1)试写出数列 的一个
的一个 项子列,并使其为等差数列;
项子列,并使其为等差数列;
(2)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等差数列,证明:
为等差数列,证明: 的公差
的公差 满足
满足 ;
;
(3)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等比数列,证明:
为等比数列,证明:
 .
.
在数列 中,前
中,前 项和为
项和为 ,
, ,则当
,则当 最小时,
最小时, 的值为( )
的值为( )
| A.5 | B.6 | C.7 | D.8 |
已知 为锐角,且
为锐角,且 ,函数
,函数 ,数列
,数列 的首项
的首项 ,
, .
.
(1)求函数 的表达式;(2)求数列
的表达式;(2)求数列 的前
的前 项和
项和 .
.
对于项数为 的有穷数列数集
的有穷数列数集 ,记
,记
 ,即
,即 为
为 、
、 、
、 、
、 中的最大值,并称数列
中的最大值,并称数列 是
是 的控制数列.如
的控制数列.如 、
、 、
、 、
、 、
、 的控制数列是
的控制数列是 、
、 、
、 、
、 、
、 .
.
(1)若各项均为正整数的数列 的控制数列为
的控制数列为 、
、 、
、 、
、 、
、 ,写出所有的
,写出所有的 ;
;
(2)设 是
是 的控制数列,满足
的控制数列,满足 (
( 为常数,
为常数, 、
、 、
、 、
、 ).求证:
).求证:
 .
.
已知数列 满足
满足
(1)若 ,数列
,数列 单调递增,求实数
单调递增,求实数 的取值范围。
的取值范围。
(2)若 ,试写出
,试写出 对任意
对任意 成立的充要条件,并证明你的结论。
成立的充要条件,并证明你的结论。
数列 共有5项,其中
共有5项,其中 ,且
,且 ,则满足条件的不同数列的个数为( )
,则满足条件的不同数列的个数为( )
| A.3 | B.4 | C.5 | D.6 |