高中数学一阶、二阶线性常系数递归数列的通项公式试题

已知数列{a_n}的前n项和S_n＝n²－7n，且满足16＜a_k＋a_k＋1＜22，则正整数k＝________.

已知函数f(x)对应关系如下表所示，数列{a_n}满足：a₁＝3，a_n＋1＝f(a_n)，则a_{2 012}＝________.

x	1	2	3
f(x)	3	2	1

设S_n为数列{a_n}的前n项和，S_n＝(－1)ⁿa_n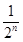－，n∈N^*，则S₁＋S₂＋S₃＋…＋S₁₀₀＝________.

若数列{a_n}的前n项和为S_n＝a_n＋，则数列{a_n}的通项公式是a_n＝________.

已知数列{a_n}满足：a₁＝，a_n＋1＝ (n∈N^*)．
(1)求a₂，a₃的值；
(2)证明：不等式0＜a_n＜a_n＋1对于任意n∈N^*都成立．

如图是见证魔术师“论证”64＝65飞神奇．对这个乍看起来颇为神秘的现象，我们运用数学知识不难发现其中的谬误．另外，我们可以更换图中的数据，就能构造出许多更加直观与“令人信服”的“论证”．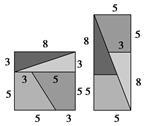

请你用数列知识归纳：(1)这些图中的数所构成的数列：________；(2)写出与这个魔术关联的一个数列递推关系式：________.

若数列{a_n}满足＝d(n∈N^*，d为常数)，则称数列{a_n}为“调和数列”．已知正项数列为“调和数列”，且b₁＋b₂＋…＋b₉＝90，则b₄·b₆的最大值是(　　)．

A．10

B．100

C．200

D．400

已知数列{a_n}满足a_n＋1＝＋，且a₁＝，则该数列的前2 013项的和等于(　　)．

A．

B．3019

C．1508

D．013

已知数列{a_n}的通项公式是a_n＝，若前n项和为10，则项数n为(　　)．

A．11

B．99

C．120

D．121

设{a_n}是公比大于1的等比数列，S_n为数列{a_n}的前n项和．已知S₃＝7，且a₁＋3,3a₂，a₃＋4构成等差数列．
(1)求数列{a_n}的通项公式；
(2)令b_n＝ln a_3n＋1，n＝1,2，…，求数列{b_n}的前n项和T_n.

设{a_n}是公比不为1的等比数列，其前n项和为S_n，且a₅，a₃，a₄成等差数列．
(1)求数列{a_n}的公比；
(2)证明：对任意k∈N^*，S_k＋2，S_k，S_k＋1成等差数列．

已知数列{a_n}的前n项和为S_n，且满足S_n＝n²，数列{b_n}满足b_n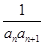＝，T_n为数列{b_n}的前n项和．
(1)求数列{a_n}的通项公式a_n和T_n；
(2)若对任意的n∈N^*，不等式λT_n<n＋(－1)ⁿ恒成立，求实数λ的取值范围．

已知数列{a_n}的通项公式是a_n＝－n²＋12n－32，其前n项和是S_n，对任意的m，n∈N^*且m<n，则S_n－S_m的最大值是(　　)．

A．－21

B．4

C．8

D．10

正项数列{a_n}的前n项和S_n满足：－(n²＋n－1)S_n－(n²＋n)＝0.
(1)求数列{a_n}的通项公式a_n；
(2)令b_n＝，数列{b_n}的前n项和为T_n，证明：对于任意的n∈N^*，都有T_n<.

设S_n为数列{a_n}的前n项和，若 (n∈N^*)是非零常数，则称该数列为“和等比数列”；若数列{c_n}是首项为2，公差为d(d≠0)的等差数列，且数列{c_n}是“和等比数列”，则d＝________.